Aufgabe 3.1: Wahrscheinlichkeiten beim Würfeln
Wir betrachten das Zufallsexperiment „Würfeln mit ein oder zwei Würfeln”. Beide Würfel sind fair (die sechs möglichen Ergebnisse sind gleichwahrscheinlich) und durch ihre Farben unterscheidbar:
- Die Zufallsgröße $R = \{1, 2, 3, 4, 5, 6 \}$ bezeichnet die Augenzahl des roten Würfels.
- Die Zufallsgröße $B = \{1, 2, 3, 4, 5, 6 \}$ bezeichnet die Augenzahl des blauen Würfels.
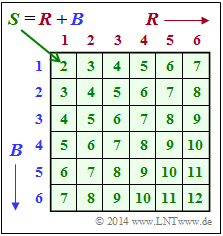
- Die Zufallsgröße $S =R + B$ steht für die Summe beider Würfel.
In dieser Aufgabe sollen verschiedene Wahrscheinlichkeiten mit Bezug zu den Zufallsgrößen $R$, $B$ und $S$ berechnet werden, wobei das oben angegebene Schema hilfreich sein kann. Dieses beinhaltet die Summe $S$ in Abhängigkeit von $R$ und $B$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
- Wiederholt wird hier insbesondere der Lehrstoff des Kapitels Wahrscheinlichkeitsrechnung im Buch „Stochastische_Signaltheorie”.
- Sollte die Eingabe des Zahlenwertes „0” erforderlich sein, so geben Sie bitte „0.” ein.
Fragebogen
Musterlösung
- mit dem roten Würfel eine „6” geworfen wird:
- $$\underline{{\rm Pr}(R=6) = 1/6} = 0.1667 \hspace{0.05cm},$$
- mit dem blauen Würfel eine „1” oder eine „2” geworfen wird:
- $$\underline{{\rm Pr}(B\le 2) = 1/3} = 0.3333 \hspace{0.05cm},$$
- beide Würfel die gleiche Augenzahl anzeigen:
- $$\underline{{\rm Pr}(R=B) = 6/36} = 0.1667 \hspace{0.05cm}.$$
Letzteres basiert auf der 2D–Darstellung auf dem Augenblatt sowie auf der „Klassischen Definition der Wahrscheinlichkeit” entsprechend K/M, wobei K = 6 der insgesamt M = 36 gleichwahrscheinlichen Elementarereignisse „R ∩ B” dem hieraus abgeleiteten Ereignis „R = B” zugeordnet werden können, die auf der Diagonalen liegen. Würfelspieler sprechen in diesem Fall von einem „Pasch”.
(2) Die Lösung basiert wieder auf der Klassischen Definition der Wahrscheinlichkeit:
- In K = 2 der M = 36 Elementarfelder steht eine „3”: Pr(S = 3) = 2/36 = 0.0556.
- In K = 6 der M = 36 Elementarfelder steht eine „7”: Pr(S = 7) = 6/36 = 0.1667.
- In K = 18 der M = 36 Felder steht eine ungerade Zahl ⇒ Pr(S ist ungerade) = 18/36 = 0.5.
Dieses letzte Ergebnis könnte man auch auf anderem Wege erhalten:
- $${\rm Pr}(S\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}) = {\rm Pr}\big [(R\hspace{0.12cm}{\rm ist\hspace{0.12cm} ungerade}) \cap (B\hspace{0.12cm}{\rm ist\hspace{0.12cm} gerade}) \big ] + {\rm Pr}\big [(R\hspace{0.12cm}{\rm ist\hspace{0.12cm} gerade}) \cap (B\hspace{0.12cm}{\rm ist\hspace{0.12cm} ungerade})\big ]\hspace{0.05cm}. $$
Mit Pr(R gerade) = Pr(R ungerade) = Pr(B gerade) = Pr(B ungerade) = 1/2 folgt daraus ebenfalls:
- $${\rm Pr}(S\hspace{0.15cm}{\rm ist \hspace{0.15cm} ungerade}) = 1/2 \cdot 1/2 + 1/2 \cdot 1/2 = 1/2 \hspace{0.05cm}.$$
(3) Die Wahrscheinlichkeit für das Ereignis, dass mindestens einer der beiden Würfel eine „6” zeigt, ist:
- $${\rm Pr}\big [(R= 6) \cup (B= 6) \big ] = K/M = 11/36 \hspace{0.15cm} \underline{= 0.3056} \hspace{0.05cm}.$$
Die zweite Wahrscheinlichkeit steht allein für den „Sechser–Pasch”:
- $${\rm Pr}\big [(R= 6) \cap (B= 6) \big ] = K/M = 1/36 \hspace{0.15cm} \underline{= 0.0278} \hspace{0.05cm}.$$
(4) Das Ergebnis für L = 1 wurde bereits in der Teilaufgabe (3) ermittelt:
- $$p_1 = {\rm Pr}\big [(R= 6) \cup (B= 6) \big ] = {11}/{36} \hspace{0.15cm} \underline{= 0.3056} \hspace{0.05cm}.$$
Die Wahrscheinlichkeit p2 lässt sich mit p1 wie folgt ausdrücken:
- $$p_2 = (1 - p_1) \cdot p_1 = \frac{25}{36} \cdot \frac{11}{36} \hspace{0.15cm} \underline{= 0.2122} \hspace{0.05cm}. $$
In Worten: Die Wahrscheinlichkeit, dass im zweiten Wurf erstmals eine „6” geworfen wird, ist gleich der Wahrscheinlichkeit, dass im ersten Wurf keine „6” geworfen wurde ⇒ Wahrscheinlichkeit (1 – p1), aber im zweiten Wurf mindestens eine „6” dabei ist ⇒ Wahrscheinlichkeit p1.
Entsprechend gilt für die Wahrscheinlichkeit „erste 6 im dritten Wurf”:
- $$p_3 = (1 - p_1)^2 \cdot p_1 = \frac{25}{36} \cdot \frac{25}{36} \cdot\frac{11}{36} \hspace{0.15cm} \underline{= 0.1474} \hspace{0.05cm}.$$
(5) Durch Erweiterung der Musterlösung zur Teilaufgabe (4) erhält man: $$\text{Pr(gerades L)}= p_2 \hspace{-0.05cm}+ \hspace{-0.05cm}p_4 \hspace{-0.05cm}+ \hspace{-0.05cm} p_6 \hspace{-0.05cm}+ \hspace{-0.05cm} ... = (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1) \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^3 \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm}(1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^5 \cdot p_1 \hspace{-0.05cm}+ \hspace{-0.05cm} \text{...} = (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1) \cdot p_1 \cdot \left [ 1 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^2 \hspace{-0.05cm}+ \hspace{-0.05cm} (1 \hspace{-0.05cm}- \hspace{-0.05cm} p_1)^4 +\text{...}\hspace{0.05cm} \right ] \hspace{0.05cm}. $$ Entsprechend erhält man für die Wahrscheinlichkeit des Komplementärereignisses:
- $${\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} ungeradzahlig}) = p_1 + p_3 + p_5 + ... = p_1 \cdot \left [ 1 + (1 - p_1)^2 + (1 - p_1)^4 + ... \hspace{0.15cm} \right ] \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} \frac{{\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} ungeradzahlig}) } {{\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} geradzahlig})} = \frac{1}{1 - p_1} \hspace{0.05cm}. $$
Weiter muss gelten:
- $${\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} geradzahlig}) + {\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} ungeradzahlig}) = 1$$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} geradzahlig}) \cdot \left [ 1 + \frac{1}{1 - p_1} \right ] = 1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\rm Pr}(L\hspace{0.15cm}{\rm ist\hspace{0.15cm} geradzahlig}) = \frac{1 - p_1}{2 - p_1} = \frac{25/36}{61/36} = \frac{25}{61} \hspace{0.15cm} \underline{= 0.4098} \hspace{0.05cm}.$$