AWGN–Kanalkapazität bei wertkontinuierlichem Eingang
Inhaltsverzeichnis
Transinformation zwischen wertkontinuierlichen Zufallsgrößen
Im Kapitel Informationstheoretisches Modell der Digitalsignalübertragung wurde die Transinformation (englisch: Mutual Information) zwischen den beiden wertdiskreten Zufallsgrößen $X$ und $Y$ unter Anderem in folgender Form angegeben:
- $$I(X;Y) = \hspace{-0.4cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.05cm} (P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ P_{XY}(x, y)}{P_{X}(x) \cdot P_{Y}(y)} \hspace{0.05cm}.$$
Diese Gleichung entspricht gleichzeitig der Kullback–Leibler–Distanz (kurz KLD) zwischen der Verbundwahrscheinlichkeitsfunktion $P_{XY}$ und dem Produkt der beiden Einzel–wahrscheinlichkeitsfunktionen $P_X$ und $P_Y$ :
- $$I(X;Y) = D(P_{XY} \hspace{0.05cm} || \hspace{0.05cm}P_{X} \cdot P_{Y}) \hspace{0.05cm}.$$
Um daraus die Transinformation $I(X; Y)$ zwischen zwei wertkontinuierlichen Zufallsgrößen $X$ und $Y$ abzuleiten, geht man wie folgt vor (Hochkommata weisen auf eine quantisierte Größe hin):
- Man quantisiert die Zufallsgrößen $X$ und $Y$ (mit den Quantisierungsintervallen ${\it Δ}x$ und ${\it Δ}y$) und erhält so die Wahrscheinlichkeitsfunktionen $P_{X′}$ und $P_{Y′}$ .
- Die „Vektoren” $P_{X′}$ und $P_{Y′}$ werden nach den Grenzübergängen ${\it Δ}x → 0, {\it Δ}y → 0$ unendlich lang, und auch die Verbund–PMF $P_{X′Y′}$ ist dann in der Fläche unendlich weit ausgedehnt.
- Durch diese Grenzübergänge ergeben sich die Wahrscheinlichkeitsdichtefunktionen der drei kontinuierlichen Zufallsgrößen entsprechend den folgenden Gleichungen:
- $$f_X(x_{\mu}) = \frac{P_{X'}(x_{\mu})}{\it \Delta_x} \hspace{0.05cm}, \hspace{0.3cm}f_Y(y_{\mu}) = \frac{P_{Y'}(y_{\mu})}{\it \Delta_y} \hspace{0.05cm}, \hspace{0.3cm}f_{XY}(x_{\mu}\hspace{0.05cm}, y_{\mu}) = \frac{P_{X'Y'}(x_{\mu}\hspace{0.05cm}, y_{\mu})}{\it \Delta_x} \cdot {\it \Delta_y} \hspace{0.05cm}.$$
- Aus der Doppelsumme in der obigen Gleichung wird nach der Umbenennung $Δx → d_x$ bzw. $Δy → d_y$ die für wertkontinuierliche Zufallsgrößen gültige Gleichung:
- $$I(X;Y) = \hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{ f_{XY}(x, y) } {f_{X}(x) \cdot f_{Y}(y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y \hspace{0.05cm}.$$
Durch Aufspaltung dieses Doppelintegrals lässt für die Transinformation auch schreiben:
- $$I(X;Y) = h(X) + h(Y) - h(XY)\hspace{0.05cm}.$$
Verwendet ist hierbei die differentielle Verbund–Entropie
- $$h(XY) = -\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} [f_{XY}(x, y) ] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y$$
sowie die beiden differentiellen Einzel–Entropien
- $$h(X) = -\hspace{-0.7cm} \int\limits_{x \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} [f_X(x)] \hspace{0.1cm}{\rm d}x \hspace{0.05cm},\hspace{0.5cm} h(Y) = -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_Y)} \hspace{-0.35cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y \hspace{0.05cm}.$$
Zur Äquivokation und Irrelevanz
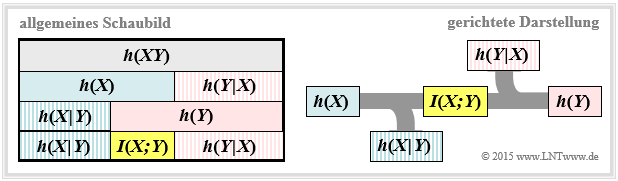
Wir gehen weiter von der wertkontinuierlichen Transinformationsgleichung $I(X;Y) = h(X) + h(Y) - h(XY)$ aus. Diese Darstellung findet sich auch im folgenden Schaubild (linke Grafik, über alle Zeilen).
Daraus erkennt man, dass die Transinformation auch noch wie folgt dargestellt werden kann:
- $$I(X;Y) = h(Y) - h(Y \hspace{-0.1cm}\mid \hspace{-0.1cm} X) =h(X) - h(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Y)\hspace{0.05cm}.$$
Diese fundamentalen informationstheoretischen Zusammenhänge kann man auch aus der rechten Grafik ablesen. Diese gerichtete Darstellung ist für Nachrichtenübertragungssysteme besonders geeignet.
Die abfließende bzw. zufließende differentielle Entropie kennzeichnen
- die Äquivokation (englisch: Equivocation):
- $$h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) =\hspace{0.2cm} -\int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \left [{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \right] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm},$$
- die Irrelevanz (englisch: Irrelevance):
- $$h(Y \hspace{-0.05cm}\mid \hspace{-0.05cm} X) =\hspace{0.2cm}- \int \hspace{-0.9cm} \int\limits_{\hspace{-0.4cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm} (\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \left [{f_{\hspace{0.03cm}Y \mid \hspace{0.03cm} X} (y \hspace{-0.05cm}\mid \hspace{-0.05cm} x)} \right] \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$
Auf die Bedeutung dieser beiden informationstheoretischen Größen wird in der Zusatzaufgabe 4.5Z noch genauer eingegangen. Vergleicht man die grafischen Darstellungen der Transinformation bei
- wertdiskreten Zufallsgrößen im Abschnitt Informationstheoretisches Modell der Digitalsignalübertragung und
- wertkontinuierlichen Zufallsgrößen entsprechend obigem Schaubild,
so erkennt man als einziges Unterscheidungsmerkmal, dass jedes „$H$” (Entropie; größer/gleich Null) durch ein „$h$” (differentielle Entropie, kann positiv, negativ oder Null sein) ersetzt wurde. Ansonsten ist die Transinformation in beiden Darstellungen gleich und es gilt stets $I(X; Y) ≥ 0$. Im Folgenden verwenden wir meist den Logarithmus dualis ⇒ „log2” und erhalten somit die Transinformation in „bit”.
Transinformationsberechnung bei additiver Störung
Wir betrachten nun ein sehr einfaches Modell der Nachrichtenübertragung:
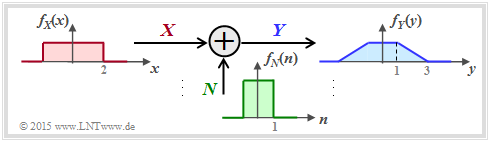
- Die Zufallsgröße $X$ steht für das (mittelwertfreie) Sendesignal und ist durch die WDF $f_X(x)$ und die Varianz $σ_X^2$ gekennzeichnet. Die Sendeleistung $P_X$ ist identisch mit $σ_X^2$.
- Die additive Störung $N$ ist durch die WDF $f_N(n)$ und die Störleistung $P_N = σ_N^2$ gegeben. Wenn $X$ und $N$ als statistisch unabhängig angenommen werden ⇒ signalunabhängiges Rauschen, gilt $\text{E}[X · N] = \text{E}[X] · \text{E}[N] = 0$ .
- Das Empfangssignal ist $Y = X + N$ Die Ausgangs–WDF $f_Y(y)$ ist mit der Faltungsoperation berechenbar ⇒ $f_Y(y) = f_X(x) ∗ f_N(n)$ und für die Empfangsleistung (Varianz) gilt:
- $$P_Y = \sigma_Y^2 = {\rm E}[Y^2] = {\rm E}[(X+N)^2] = {\rm E}[X^2] + {\rm E}[N^2] = \sigma_X^2 + \sigma_N^2 = P_X + P_N \hspace{0.05cm}.$$
Die in der nachfolgenden Grafik eingezeichneten Dichtefunktionen (rechteck– bzw. trapezförmig) sollen nur den Rechengang verdeutlichen und haben keine praktische Relevanz.
Zur Berechnung der Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ gibt es entsprechend dem Schaubild auf der vorherigen Seite drei Möglichkeiten:
- Berechnung entsprechend $I(X, Y) = h(X) + h(Y) – h(XY)$:
- Die beiden ersten Terme sind aus $f_X(x)$ bzw. $f_Y(y)$ in einfacher Weise berechenbar. Problematisch ist die differentielle Verbundentropie $h(XY)$. Hierzu benötigt man die 2D–Verbund–WDF $f_{XY}(x, y)$, die meist nicht direkt gegeben ist.
- Berechnung entsprechend $I(X, Y) = h(Y) – h(Y|X)$:
- Hierbei bezeichnet $h(Y|X)$ die differentielle Streuentropie. Es gilt $h(Y|X) = h(X + N|X) = h(N)$, so dass $I(X; Y)$ bei Kenntnis von $f_X(x)$ und $f_N(n)$ über die Gleichung $f_Y(y) = f_X(x) ∗ f_N(n)$ sehr einfach zu berechnen ist.
- Berechnung entsprechend $I(X, Y) = h(X) – h(X|Y)$:
- Nach dieser Gleichung benötigt man allerdings die differentielle Rückschlussentropie $h(X|Y)$, die schwieriger angebbar ist als $h(Y|X)$.
Resümée: Im Folgenden schreiben wir für die Transinformation zwischen dem Eingang $X$ und dem Ausgang $Y$ eines Nachrichtenübertragungssystems bei additiver und unkorrelierter Störung $N$:
- $$I(X;Y) \hspace{-0.05cm} = \hspace{-0.01cm} h(Y) \hspace{-0.01cm}- \hspace{-0.01cm}h(N) \hspace{-0.01cm}=\hspace{-0.05cm} -\hspace{-0.7cm} \int\limits_{y \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_Y)} \hspace{-0.65cm} f_Y(y) \cdot {\rm log} \hspace{0.1cm} [f_Y(y)] \hspace{0.1cm}{\rm d}y +\hspace{-0.7cm} \int\limits_{n \hspace{0.05cm}\in \hspace{0.05cm}{\rm supp}(f_N)} \hspace{-0.65cm} f_N(n) \cdot {\rm log} \hspace{0.1cm} [f_N(n)] \hspace{0.1cm}{\rm d}n\hspace{0.05cm}.$$
Kanalkapazität des AWGN–Kanals
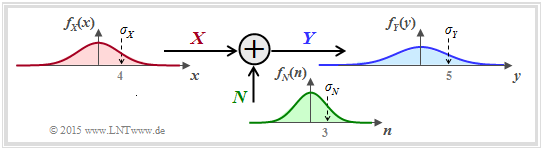
Spezifiziert man im bisherigen Systemmodell die Wahrscheinlichkeitsdichtefunktion der Störung (bzw. des Rauschens) zu
- $$f_N(n) = \frac{1}{\sqrt{2\pi \sigma_N^2}} \cdot {\rm exp}\left [ - \hspace{0.05cm}\frac{n^2}{2 \sigma_N^2} \right ] \hspace{0.5cm} {\rm mit } \hspace{0.5cm}\sigma_N^2 = P_N\hspace{0.05cm}, $$
so erhalten wir das folgende Modell zur Berechnung der Kanalkapazität des so genannten AWGN–Kanals (Additive White Gaussian Noise).
Aus vorherigen Abschnitten wissen wir:
- Die Kanalkapazität $C_{\rm AWGN}$ gibt die maximale Transinformation $I(X; Y)$ zwischen der Eingangsgröße $X$ und der Ausgangsgröße $Y$ des AWGN–Kanals an.
- Die Maximierung bezieht sich dabei auf die bestmögliche Eingangs–WDF. Somit gilt unter der Nebenbedingung der Leistungsbegrenzung:
- $$C_{\rm AWGN} = \max_{f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} I(X;Y) = -h(N) + \max_{f_X:\hspace{0.05cm} {\rm E}[X^2] \le P_X} \hspace{-0.35cm} h(Y) \hspace{0.05cm}.$$
Hier ist bereits berücksichtigt, dass sich die Maximierung allein auf die differentielle Entropie $h(Y)$ ⇒ WDF $f_Y(y)$ bezieht. Bei gegebener Störleistung $P_N$ ist nämlich $h(N) = 1/2 · \log_2 (2π{\rm e} · P_N)$ eine Konstante.
- Das Maximum für $h(Y)$ erhält man für eine Gaußsche WDF $f_Y(y)$, wobei $P_Y = P_X + P_N$ zu setzen ist, siehe Seite Maximale differentielle Entropie bei Leistungsbegrenzung:
- $${\rm Max}[h(Y)] = 1/2 · \log_2 [2πe · (P_X + P_N)].$$
- Die Ausgangs–WDF $f_Y(y) = f_X(x) ∗ f_N(n)$ ist aber nur dann gaußförmig, wenn sowohl $f_X(x)$ als auch $f_N(n)$ Gaußfunktionen sind. Ein plakativer Merkspruch zur Faltungsoperation lautet nämlich: „Gauß bleibt Gauß, und Nicht–Gauß wird nie (exakt) Gauß”.
Resümée: Beim AWGN–Kanal ⇒ Gaußsche Rausch-WDF $f_N(n)$ ergibt sich die Kanalkapazität genau dann, wenn die Eingangs–WDF $f_X(x)$ ebenfalls gaußförmig ist:
- $$C_{\rm AWGN} = h_{\rm max}(Y) - h(N) = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_Y}{P_N} = 1/2 \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{P_N}) \hspace{0.05cm}.$$
Die Tabelle zeigt numerische Ergebnisse zur AWGN–Kanalkapazität für verschiedene Quotienten $P_X/P_N$.
Parallele Gaußsche Kanäle
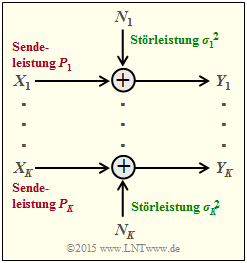
Wir betrachten nun $K$ parallele Gaußkanäle entsprechend der nebenstehenden Grafik
- von $X_1 → Y_1$, ... ,
- von $X_k → Y_k$, ... ,
- von $X_K → Y_K$.
Die Sendeleistungen in den $K$ Kanälen nennen wir
- $$P_1 = \text{E}[X_1^2], ... , P_k = \text{E}[X_k^2], ... , P_K = \text{E}[X_K^2].$$
Die $K$ Störleistungen können ebenfalls unterschiedlich sein:
- $$σ_1^2, ... , σ_k^2, ... , σ_K^2.$$
Gesucht ist nun die maximale Transinformation $I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) $ zwischen
- den $K$ Eingangsgrößen $X_1$, ... , $X_K$, sowie
- den $K$ Ausgangsgrößen $Y_1$, ... , $Y_K$,
die wir als die Gesamt–Kanalkapazität dieser AWGN–Konfiguration bezeichnen. Ausgegangen wird von Leistungsbegrenzung des Gesamtsystems. Das heißt: Die Summe aller Leistungen $P_k$ in den $K$ Einzelkanälen darf den vorgegebenen Wert $P_X$ nicht überschreiten:
- $$P_1 + ... \hspace{0.05cm}+ P_K = \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm}{\rm E} \left [ X_k^2\right ] \le P_{X} \hspace{0.05cm}.$$
Unter der nur wenig einschränkenden Annahme unabhängiger Störquellen $N_1$, ... , $N_K$ kann für die Transinformation nach einigen Zwischenschritten geschrieben werden:
- $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) = h(Y_1, ... \hspace{0.05cm}, Y_K ) - \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} h(N_k)\hspace{0.05cm}.$$
Dafür kann folgende obere Schranke angegeben werden:
- $$I(X_1, ... \hspace{0.05cm}, X_K\hspace{0.05cm};\hspace{0.05cm}Y_1, ... \hspace{0.05cm}, Y_K) \hspace{0.2cm} \le \hspace{0.1cm} \hspace{0.1cm} \sum_{k= 1}^K \hspace{0.1cm} [h(Y_k - h(N_k)] \hspace{0.2cm} \le \hspace{0.1cm} 1/2 \cdot \sum_{k= 1}^K \hspace{0.1cm} {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_k}{\sigma_k^2}) \hspace{0.05cm}.$$
- Das Gleichheitszeichen (Identität) gilt bei mittelwertfreien Gaußschen Eingangsgrößen $X_k$ sowie bei statistisch voneinander unabhängigen Störungen $N_k$.
- Man kommt von dieser Gleichung zur maximalen Transinformation ⇒ Kanalkapazität, wenn man die gesamte Sendeleistung $P_X$ unter Berücksichtigung der unterschiedlichen Störungen in den einzelnen Kanälen ( $σ_k^2$ ) bestmöglich aufteilt.
- Dieses Optimierungsproblem lässt sich wieder mit dem Verfahren der Lagrange–Multiplikatoren elegant lösen. Das folgende Beispiel erläutert nur das Ergebnis.
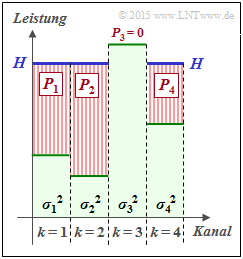
Beispiel: Wir betrachten $K$ = 4 parallele Gaußkanäle mit vier unterschiedlichen Störleistungen $σ_1^2$, ... , $σ_4^2$ gemäß der nebenstehenden Abbildung (grüne Hinterlegung).
- Gesucht ist die bestmögliche Aufteilung der Sendeleistung auf die vier Kanäle.
- Würde man dieses Profil langsam mit Wasser auffüllen, so würde das Wasser zunächst nur in den Kanal 2 fließen.
- Gießt man weiter, so sammelt sich auch im Kanal 1 etwas Wasser an und später auch im Kanal 4.
Die eingezeichnete „Wasserhöhe” $H$ beschreibt genau den Zeitpunkt, zu dem die Summe $P_1 + P_2 + P_4$ der insgesamt zur Verfügung stehenden Sendeleistung $P_X$ entspricht:
- Die optimale Leistungsaufteilung für dieses Beispiel ergibt $P_2 > P_1 > P_4$ sowie $P_3 = 0$.
- Erst bei größerer Sendeleistung $P_X$ würde auch dem dritten Kanal eine kleine Leistung $P_3$ zugewiesen.
Man bezeichnet dieses Allokationsverfahren als Water–Filling–Algorithmus.
Werden alle $K$ Gaußkanäle in gleicher Weise gestört ⇒ $σ_1^2 = ... = σ_K^2 = P_N$, so sollte man natürlich die gesamte zur Verfügung stehende Sendeleistung $P_X$ gleichmäßig auf alle Kanäle verteilen: $P_k = P_X/K$. Für die Gesamtkapazität erhält man dann:
- $$C_{\rm Gesamt} = \frac{ K}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac{P_X}{K \cdot P_N}) \hspace{0.05cm}.$$
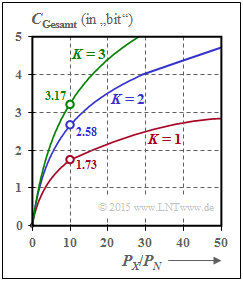
Die rechte Grafik zeigt die Gesamtkapazität als Funktion des Quotienten $P_X/P_N$ für $K = 1$, $K = 2$ und $K = 3$:
- Bei $P_X/P_N = 10 ⇒ 10 · \text{lg} (P_X/P_N) = 10 ß \text{dB}$ wird die Gesamtkapazität um ca. 50% größer, wenn man die Gesamtleistung auf zwei Kanäle gleichmäßig aufteilt.
- Im Grenzfall $P_X/P_N → ∞$ nimmt die Gesamtkapazität um den Faktor $K$ zu ⇒ Verdoppelung mit $K = 2$.
Die beiden identischen und voneinander unabhängigen Kanäle kann man auf unterschiedliche Weise realisieren, zum Beispiel durch Zeit–, Frequenz– oder Raummultiplexverfahren.
Der Fall $K = 2$ lässt sich aber auch durch die Verwendung orthogonaler Basisfunktionen wie „Cosinus” und „Sinus” verwirklichen wie zum Beispiel bei
- der Quadratur–Amplitudenmodulation (QAM) oder
- einer mehrstufigen Phasenmodulation wie QPSK oder 8–PSK.