Beschreibungsgrößen digitaler Kanalmodelle

1. Digitalsignalübertragung
2. Digitale Kanalmodelle
3. Beschreibungsgrößen digitaler Kanalmodelle

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

# ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL #

Zum Abschluss dieses Buches „Digitalsignalübertragung” werden Digitale Kanalmodelle behandelt, die das Übertragungsverhalten eines digitalen Übertragungssystems nicht sehr detailliert entsprechend den einzelnen Systemkomponenten beschreiben, sondern eher global anhand typischer Fehlerstrukturen. Solche Kanalmodelle verwendet man vor allem bei kaskadierten Übertragungssystemen für den inneren Block, wenn die Leistungsfähigkeit der äußeren Systemkomponenten – beispielsweise Coder und Decoder – per Simulation ermittelt werden sollen. Im Einzelnen werden behandelt:

• die Beschreibungsgrößen Fehlerkorrelationsfunktion und Fehlerabstandsverteilung,
• das BSC–Modell (Binary Symmetric Channel) zur Beschreibung statistisch unabhängiger Fehler,
• die Bündelfehler–Kanalmodelle nach Gilbert–Elliott und McCullough,
• das Wilhelm–Kanalmodell zur formelmäßigen Approximation von gemessenen Fehlerkurven,
• einige Hinweise zur Generierung von Fehlerfolgen, zum Beispiel hinsichtlich Fehlerabstandssimulation,
• die Auswirkungen der verschiedenen Fehlerstrukturen auf BMP–Dateien   ⇒   Bilder und WAV–Dateien   ⇒   Audios.

Hinweis: Alle BMP–Bilder und WAV–Audios zu diesem Kapitel wurden mit dem Windows–Programm „Digitale Kanalmodelle & Multimedia” aus dem (früheren) Praktikum „Simulation Digitaler Übertragungssysteme ” am Lehrstuhl für Nachrichtentechnik der TU München erzeugt. Die folgenden Links stellen bereit:

• das Windows-Programm DKM  ⇒  Link verweist auf die ZIP-Version des Programms; und
• die zugehörige Praktikumsanleitung  ⇒  Link verweist auf die PDF-Version.

In diesem Offline–Versuch finden Sie weitere Aufgaben und Simulationen zu den „Digitalen Kanalmodellen”.

Anwendung analoger Kanalmodelle

Für Untersuchungen von Nachrichtenübertragungssystemen sind geeignete Kanalmodelle von großer Wichtigkeit, weil diese

• Voraussetzung für eine Systemsimulation und –optimierung sind, sowie
  
• gleichbleibende und rekonstruierbare Randbedingungen schaffen.
  
  

Für die Digitalsignalübertragung gibt es sowohl analoge als auch digitale Kanalmodelle: Ein analoges Kanalmodell muss zwar den Übertragungskanal nicht in allen physikalischen Einzelheiten wiedergeben, sollte jedoch dessen Übertragungsverhalten inklusive der dominanten Störgrößen funktionell ausreichend genau beschreiben. Meist muss ein Kompromiss zwischen mathematischer Handhabbarkeit und dem Bezug zur Realität gefunden werden.

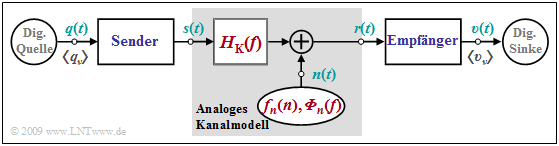
$\text{Beispiel 1:}$  Die Grafik zeigt ein analoges Kanalmodell innerhalb eines digitalen Übertragungssystems. Dieses beinhaltet

• den Kanalfrequenzgang $H_{\rm K}(f)$ zur Beschreibung der linearen Verzerrungen, sowie
• ein additives Störsignal $n(t)$, charakterisiert durch die Wahrscheinlichkeitsdichtefunktion (WDF) $f_n(n)$ und das Leistungsdichtespektrum (LDS) ${\it \Phi}_n(f)$.
  

Analoges Kanalmodell innerhalb eines digitalen Übertragungssystems

Ein Sonderfall dieses Modells ist der so genannte AWGN–Kanal (Additive White Gaussian Noise) mit den Systemeigenschaften

\[H_{\rm K}(f) = 1\hspace{0.05cm},\hspace{0.2cm}{\it \Phi}_{n}(f) = {\rm const.}\hspace{0.05cm},\hspace{0.2cm} {f}_{n}(n) = \frac{1}{\sqrt{2 \pi} \cdot \sigma} \cdot {\rm e}^{-n^2\hspace{-0.05cm}/(2 \sigma^2)}\hspace{0.05cm}.\]

Dieses einfache Modell eignet sich zum Beispiel zur Beschreibung eines Funkkanals mit zeitinvariantem Verhalten, wobei das Kanalmodell dahingehend abstrahiert ist, dass

• der eigentlich bandpassartige Kanal im äquivalenten Tiefpassbereich beschrieben wird, und
  

• die vom Frequenzband und der Übertragungsweglänge abhängige Dämpfung mit der Varianz $\sigma^2$ des Rauschsignals $n(t)$ verrechnet wird.
  

Zur Berücksichtigung zeitvarianter Eigenschaften muss man andere Modelle wie Rayleigh–Fading, Rice–Fading und Lognormal–Fading verwenden, die im Buch „Mobile Kommunikation” beschrieben werden.

Bei leitungsgebundenen Übertragungssystemen ist insbesondere der spezifische Frequenzgang des Übertragungsmediums entsprechend den Angaben für Koaxialkabel und Zweidrahtleitung im Buch „Lineare zeitinvariante Systeme” zu berücksichtigen, aber auch, dass aufgrund von Fremdstörungen (Nebensprechen, elektromagnetische Felder, usw.) nicht mehr von Weißem Rauschen ausgegangen werden kann.

Bei optischen Systemen muss zudem das multiplikativ wirkende, also signalabhängige Schrotrauschen geeignet in das analoge Kanalmodell eingearbeitet werden.

Definition digitaler Kanalmodelle

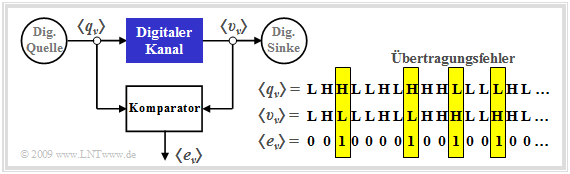
Ein analoges Kanalmodell zeichnet sich durch analoge Eingangs– und Ausgangsgrößen aus. Dagegen sind bei einem digitalen Kanalmodell (manchmal auch als „diskret” bezeichnet) sowohl der Eingang als auch der Ausgang zeit– und wertdiskret. Im Folgenden seien dies die Quellensymbolfolge $ \langle q_\nu \rangle$ mit $ q_\nu \in \{\rm L, \ H\}$ und die Sinkensymbolfolge $ \langle v_\nu \rangle$ mit $ v_\nu \in \{\rm L, \ H\}$. Die Laufvariable $\nu$ kann Werte zwischen $1$ und $N$ annehmen.

Digitales Kanalmodell und beispielhafte Folgen

Wie ein Vergleich mit dem Blockschaltbild auf der letzten Seite zeigt, ist der Digitale Kanal ein vereinfachendes Modell des analogen Übertragungskanals einschließlich der technischen Sende– und Empfangseinrichtungen. Vereinfachend deshalb, weil dieses Modell sich lediglich auf die auftretenden Übertragungsfehler bezieht, dargestellt durch die Fehlerfolge $ \langle e_\nu \rangle$ mit

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

Während $\rm L$ und $\rm H$ die möglichen Symbole bezeichnen, die hier für Low und High stehen, ist $ e_\nu \in \{\rm 0, \ 1\}$ ein reeller Zahlenwert. Oft werden die Symbole auch als $ q_\nu \in \{\rm 0, \ 1\}$ und $ v_\nu \in \{\rm 0, \ 1\}$ definiert. Um Verwechslungen zu vermeiden, haben wir hier die etwas ungewöhnliche Nomenklatur verwendet.

Die in der Grafik angegebene Fehlerfolge $ \langle e_\nu \rangle$

• ergibt sich durch den Vergleich der beiden Binärfolgen $ \langle q_\nu \rangle$ und $ \langle v_\nu \rangle$,
  
• beinhaltet nur Informationen über die Abfolge der Übertragungsfehler und damit weniger Information als ein analoges Kanalmodell,
  
• wird zweckmäßigerweise durch einen Zufallsprozess mit nur wenigen Parametern angenähert.
  
  

$\text{Fazit:}$  Die Fehlerfolge $ \langle e_\nu \rangle$ erlaubt Aussagen über die Fehlerstatistik, zum Beispiel ob es sich um so genannte

• statistisch unabhängige Fehler, oder
  

• Bündelfehler
  
  

handelt. Das folgende Beispiel soll diese beiden Fehlerarten verdeutlichen.

$\text{Beispiel 2:}$  In der folgenden Grafik sehen wir in der Mitte das BMP–Bild „Weiß” mit 300 x 200 Pixeln. Das linke Bild zeigt die Verfälschung mit statistisch unabhängigen Fehlern   ⇒   BSC–Modell, während das rechte Bild einen Bündelfehlerkanal   ⇒   Gilbert–Elliott–Modell verdeutlicht.

BMP–Bild „Weiß” mit unabhängigen Fehlern bzw. Bündelfehlern

Anzumerken ist, dass BMP–Grafiken stets zeilenweise abgespeichert werden, was im rechten Bild zu erkennen ist. Die mittlere Fehlerwahrscheinlichkeit beträgt in beiden Fällen $2.5\%$, das heißt, dass im Mittel jedes 40. Pixel verfälscht (hier: weiß ⇒ schwarz) ist.

Beispielhafte Anwendung von digitalen Kanalmodellen

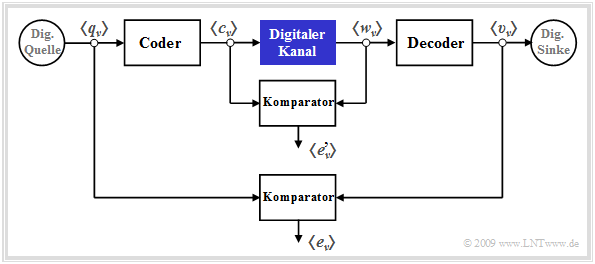
Digitale Kanalmodelle finden vorzugsweise Anwendung bei einer kaskadierten Übertragung, wie in der folgenden Grafik dargestellt.

Modell eines Übertragungssystems mit Coder/Decoder

Man erkennt aus dieser Darstellung:

• Das innere Übertragungssystem – bestehend aus Modulator, Analogkanal, Störung, Demodulator, Empfangsfilter, Entscheider und Taktrückgewinnung – ist im blau markierten Block „Digitaler Kanal” zusammengefasst.
  

• Dieser innere Block wird auschließlich durch seine Fehlerfolge $ \langle e_\nu' \rangle$ charakterisiert, die sich auf die Symbolfolgen $ \langle c_\nu \rangle$ und $ \langle w_\nu \rangle$ bezieht. Es ist offensichtlich, dass dieses digitale Kanalmodell weniger Informationen liefert als ein detailliertes Analogmodell unter Berücksichtigung aller Komponenten.

• Dagegen bezieht sich die „äußere” Fehlerfolge $ \langle e_\nu \rangle$ auf die Quellensymbolfolge $ \langle q_\nu \rangle$ und die Sinkensymbolfolge $ \langle v_\nu \rangle$ und damit auf das Gesamtsystem einschließlich der spezifischen Codierung und des empfängerseitigen Decoders.
  

• Der Vergleich der beiden Fehlerfolgen mit und ohne Berücksichtigung von Coder/Decoder erlaubt Rückschlüsse auf die Effizienz des zugrundeliegenden Codierverfahrens. Dieses ist dann und nur dann sinnvoll, wenn der äußere Komparator im Mittel weniger Fehler anzeigt als der innere.
  

Fehlerfolge und mittlere Fehlerwahrscheinlichkeit

$\text{Definition:}$  Das Übertragungsverhalten eines Binärsystems wird durch die Fehlerfolge $ \langle e_\nu \rangle$ vollständig beschrieben:

\[e_{\nu} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} {\rm falls}\hspace{0.15cm}\upsilon_\nu \ne q_\nu \hspace{0.05cm}, \\ {\rm falls}\hspace{0.15cm} \upsilon_\nu = q_\nu \hspace{0.05cm}.\\ \end{array}\]

Hieraus lässt sich die (mittlere) Bitfehlerwahrscheinlichkeit wie folgt berechnen:

\[p_{\rm M} = {\rm E}[e] = \lim_{N \rightarrow \infty} \frac{1}{N} \sum_{\nu = 1}^{N}e_{\nu}\hspace{0.05cm}.\]

Vorausgesetzt ist hierbei, dass der die Fehlentscheidungen erzeugende Zufallsprozess stationär und ergodisch ist, so dass man die Fehlerfolge $ \langle e_\nu \rangle$ formal auch durch die Zufallsgröße $e \in \{0, \ 1\}$ vollständig beschreiben kann. Der Übergang von der Zeit– zur Scharmittelung ist also zulässig.

Hinweis: In allen anderen Büchern von LNTwww wird die mittlere Bitfehlerwahrscheinlichkeit mit $p_{\rm B}$ bezeichnet. Zur Vermeidung von Verwechslungen im Zusammenhang mit dem Gilbert–Elliott–Modell ist diese hier vorgenommene Umbenennung unvermeidbar und wir sprechen nachfolgend nicht mehr von der Bitfehlerwahrscheinlichkeit, sondern nur noch von der mittleren Fehlerwahrscheinlichkeit $p_{\rm M}$.

Fehlerkorrelationsfunktion

$\text{Definition:}$  Eine wichtige Beschreibungsgröße der digitalen Kanalmodelle ist auch die Fehlerkorrelationsfunktion – abgekürzt FKF:

\[\varphi_{e}(k) = {\rm E}[e_{\nu} \cdot e_{\nu + k}] = \overline{e_{\nu} \cdot e_{\nu + k} }\hspace{0.05cm}.\]

Diese weist folgende Eigenschaften auf:

• $\varphi_{e}(k) $ gibt die (zeitdiskrete) Autokorrelationsfunktion der ebenfalls zeitdiskreten Zufallsgröße $e$ an. Die überstreichende Linie in der rechten Gleichung kennzeichnet die Zeitmittelung.
  

• Der Fehlerkorrelationswert $\varphi_{e}(k) $ liefert statistische Aussagen bezüglich zwei um $k$ auseinander liegende Folgenelemente, zum Beispiel über $e_{\nu}$ und $e_{\nu+ k}$. Die dazwischen liegenden Elemente $e_{\nu+ 1}$, ... , $e_{\nu+ k-1}$ beeinflussen den $\varphi_{e}(k) $–Wert nicht.
  

• Bei stationren Folgen gilt unabhängig von der der Fehlerstatistik wegen $e \in \{0, \ 1\}$ stets:

\[\varphi_{e}(k = 0) = {\rm E}[e_{\nu} \cdot e_{\nu}] = {\rm E}[e^2]= {\rm E}[e]= {\rm Pr}(e = 1)= p_{\rm M}\hspace{0.05cm},\]

\[\varphi_{e}(k \rightarrow \infty) = {\rm E}[e_{\nu}] \cdot {\rm E}[e_{\nu + k}] = p_{\rm M}^2\hspace{0.05cm}.\]

• Die Fehlerkorrelationsfunktion ist eine zumindest schwach abfallende Funktion. Je langsamer der Abfall der FKF–Werte erfolgt, desto länger ist das Gedächtnis des Kanals und um so weiter reichen die statistischen Bindungen der Fehlerfolge.
  
  

$\text{Beispiel 3:}$  Bei einer Binärübertragung werden $100$ der insgesamt $N = 10^5$ übertragenen Binärsymbole verfälscht, so dass die Fehlerfolge $ \langle e_\nu \rangle$ aus $100$ Einsen und $99900$ Nullen besteht.

• Die mittlere Fehlerwahrscheinlichkeit beträgt somit $p_{\rm M} =10^{-3}$.
• Die Fehlerkorrelationsfunktion $\varphi_{e}(k)$ beginnt bei $p_{\rm M} =10^{-3}$ (für $k = 0$) beginnt und tendiert für sehr große $k$–Werte gegen $p_{\rm M}^2 =10^{-6}$ (für $k = \to \infty$).
• Über den tatsächlichen Verlauf von $\varphi_{e}(k)$ ist mit den hier gemachten Angaben keine Aussage möglich.

Zusammenhang zwischen Fehlerfolge und Fehlerabstand

Zur Definition des Fehlerabstands

$\text{Definition:}$  Als Fehlerabstand $a$ bezeichnet man die Anzahl der zwischen zwei Kanalfehlern richtig übertragenen Symbole plus 1. Die Grafik verdeutlicht diese Definition.

• Jede in der Fehlerfolge $ \langle e_\nu \rangle$ enthaltene Information über das Übertragungsverhalten des digitalen Kanals ist auch in der Folge $ \langle a_n \rangle$ der Fehlerabstände enthalten.
• Da die Folgen $ \langle e_\nu \rangle$ und $ \langle a_{\nu'} \rangle$ nicht synchron laufen, verwenden wir unterschiedliche Indizes ($\nu$ bzw. $\nu'$).

Aus der Grafik erkennt man insbesondere:

• Da das erste Symbol richtig übertragen wurde $(e_1 = 0)$ und das zweite falsch $(e_2 = 1)$ , ist der Fehlerabstand $a_1 = 2$.
  

• $a_2 = 4$ sagt aus, dass zwischen den beiden ersten Fehlern $(e_2 = 1, \ e_5 = 1)$ drei Symbole richtig übertragen wurden.
  

• Folgen zwei Fehler direkt aufeinander, so ist der Fehlerabstand wie $a_3$ in obiger Grafik gleich $1$.
  

• Das Ereignis „$a = k$” bedeutet gleichzeitig $k-1$ fehlerfreie Symbole zwischen zwei Fehlern. Ist zum Zeitpunkt $\nu$ ein Fehler aufgetreten, so folgt der nächste Fehler genau zum Zeitpunkt $\nu + k$.
  

• Der Wertevorrat der Zufallsgröße $a$ ist die Menge der natürlichen Zahlen im Gegensatz zur binären Zufallsgröße $e$:

\[a \in \{ 1, 2, 3, ... \}\hspace{0.05cm}, \hspace{0.5cm}e \in \{ 0, 1 \}\hspace{0.05cm}.\]

• Die mittlere Fehlerwahrscheinlichkeit lässt sich aus beiden Zufallsgrößen ermitteln:

\[{\rm E}[e] = {\rm Pr}(e = 1) =p_{\rm M}\hspace{0.05cm}, \hspace{0.5cm} {\rm E}[a] = \sum_{k = 1}^{\infty} k \cdot {\rm Pr}(a = k) = {1}/{p_{\rm M}}\hspace{0.05cm}.\]

$\text{Beispiel 4:}$  In der skizzierten Folge sind $16$ der insgesamt $N = 40$ Symbole verfälscht   ⇒   $p_{\rm M} = 0.4$. Der Erwartungswert der Fehlerabstände ergibt entsprechend

\[{\rm E}[a] = 1 \cdot {4}/{16}+ 2 \cdot {5}/{16}+ 3 \cdot {4}/{16}+4 \cdot {1}/{16}+5 \cdot {2}/{16}= 2.5 = {1}/{p_{\rm M} }\hspace{0.05cm}.\]

Fehlerabstandsverteilung

Die Wahrscheinlichkeitsdichtefunktion (WDF) der diskreten Zufallsgröße $a \in \{1, 2, 3, \text{...}\}$ setzt sich entsprechend dem Kapitel WDF-Definition für diskrete Zufallsgrößen im Buch „Stochastische Signaltheorie” aus einer (unendlichen) Summe von Diracfunktionen zusammen:

\[f_a(a) = \sum_{k = 1}^{\infty} {\rm Pr}(a = k) \cdot \delta (a-k)\hspace{0.05cm}.\]

Wir bezeichnen diese spezielle WDF als Fehlerabstandsdichtefunktion. Die Wahrscheinlichkeit, dass der Fehlerabstand $a$ exakt gleich $k$ ist, lässt sich anhand der Fehlerfolge durch die folgende bedingte Wahrscheinlichkeit ausdrücken:

\[{\rm Pr}(a = k) = {\rm Pr}(e_{\nu + 1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm} ... \hspace{0.15cm}\cap \hspace{0.15cm}\hspace{0.05cm} e_{\nu + k -1} = 0 \hspace{0.15cm}\cap \hspace{0.15cm}e_{\nu + k} = 1 \hspace{0.1cm}| \hspace{0.1cm} e_{\nu } = 1)\hspace{0.05cm}.\]

Im Buch „Stochastische Signaltheorie” finden Sie ebenfalls die Definition der Verteilungsfunktion der diskreten Zufallsgröße $a$:

\[F_a(k) = {\rm Pr}(a \le k) \hspace{0.05cm}.\]

Diese Funktion ergibt sich aus der WDF $f_a(a)$ durch Integration von $1$ bis $k$. Die Funktion $F_a(k)$ kann Werte zwischen $0$ und $1$ (einschließlich dieser beiden Grenzen) annehmen und ist schwach monoton ansteigend.

Im Zusammenhang mit den digitalen Kanalmodellen wird in der Literatur von dieser üblichen Definition abgewichen.

$\text{Definition:}$  Vielmehr gibt hier die Fehlerabstandsverteilung (FAV) die Wahrscheinlichkeit an, dass der Fehlerabstand $a$ größer oder gleich $k$ ist:

\[V_a(k) = {\rm Pr}(a \ge k) = 1 - \sum_{\kappa = 1}^{k} {\rm Pr}(a = \kappa)\hspace{0.05cm}.\]

Insbesondere gilt:   $V_a(k = 1) = 1 \hspace{0.05cm},\hspace{0.5cm}\lim_{k \rightarrow \infty}V_a(k ) = 0 \hspace{0.05cm}.$

Zwischen der monoton ansteigenden Funktion $F_a(k)$ und der monoton abfallenden Funktion $V_a(k)$ gilt folgender Zusammenhang:

\[F_a(k ) = 1-V_a(k +1) \hspace{0.05cm}.\]

Diskrete Wahrscheinlichkeitsdichte und Verteilungsfunktionen

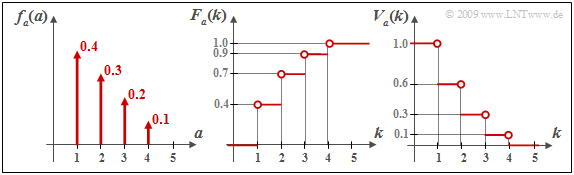
$\text{Beispiel 5:}$  Die Grafik zeigt eine willkürliche diskrete Fehlerabstandsdichtefunktion $f_a(a)$   ⇒   linke Skizze und die daraus resultierenden kumulativen Funktionen

• $F_a(k ) = {\rm Pr}(a \le k)$   ⇒   mittlere Skizze, sowie
• $V_a(k ) = {\rm Pr}(a \ge k)$   ⇒   rechte Skizze.
  

Beispielsweise ergibt sich für $k = 2$:

\[F_a( k =2 ) = {\rm Pr}(a = 1) + {\rm Pr}(a = 2) \hspace{0.05cm}, \]

\[\Rightarrow \hspace{0.3cm} F_a( k =2 ) = 1-V_a(k = 3)= 0.7\hspace{0.05cm}, \]

\[ V_a(k =2 ) = 1 - {\rm Pr}(a = 1) \hspace{0.05cm},\]

\[\Rightarrow \hspace{0.3cm} V_a(k =2 ) = 1-F_a(k = 1) = 0.6\hspace{0.05cm}.\]

Für $k = 4$ erhält man folgende Resultate:

\[F_a(k = 4 ) = {\rm Pr}(a \le 4) = 1 \hspace{0.05cm}, \hspace{0.5cm} V_a(k = 4 ) = {\rm Pr}(a \ge 4)= {\rm Pr}(a = 4) = 0.1 = 1-F_a(k = 3) \hspace{0.05cm}.\]

Aufgaben zum Kapitel

A5.1 Fehlerabstandsverteilung

5.2 Fehlerkorrelationsfunktion