Zeitdiskrete Signaldarstellung

Inhaltsverzeichnis

1 # ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL #
2 Prinzip und Motivation
3 Zeitbereichsdarstellung
4 Diracpuls im Zeit- und im Frequenzbereich
5 Frequenzbereichsdarstellung
6 Signalrekonstruktion
7 Das Abtasttheorem
8 Aufgaben zum Kapitel

# ÜBERBLICK ZUM FÜNFTEN HAUPTKAPITEL #

Voraussetzung für die systemtheoretische Untersuchung von Digitalsystemen oder für deren Computersimulation ist eine geeignete zeitdiskrete Signalbeschreibung.

Dieses Kapitel verdeutlicht den mathematischen Übergang von zeitkontinuierlichen auf zeitdiskrete Signale, wobei von Fouriertransformation und Fourierrücktransformation ausgegangen wird.

Das Kapitel beinhaltet im Einzelnen:

die Zeit- und Frequenzbereichsdarstellung zeitdiskreter Signale,
das Abtasttheorem, das bei der Zeitdiskretisierung unbedingt zu beachten ist,
die Rekonstruktion des Analogsignals aus der zeitdiskreten Repräsentation,
die Diskrete Fouriertransformation (DFT) und deren Inverse (IDFT),
die Fehlermöglichkeiten bei Anwendung von DFT und IDFT,
die Anwendung der Spektralanalyse zur Verbesserung messtechnischer Verfahren, und
den für eine Rechnerimplementierung besonders geeigneten FFT-Algorithmus.

Weitere Informationen zum Thema sowie Aufgaben, Simulationen und Programmierübungen finden Sie im

Kapitel 7: Diskrete Fouriertransformation, Programm dft,
Kapitel 8: Spektralanalyse, Programm stp, und
Kapitel 12: Pulscodemodulation, Programm pcm

des Praktikums „Simulationsmethoden in der Nachrichtentechnik”. Diese (ehemalige) LNT-Lehrveranstaltung an der TU München basiert auf

dem Lehrsoftwarepaket LNTsim ⇒ Link verweist auf die ZIP-Version des Programms,
der Praktikumsanleitung - Teil A ⇒ Link verweist auf die PDF-Version; Kapitel 7: Seite 119-144, Kapitel 8: Seite 145-164, und
der Praktikumsanleitung - Teil B ⇒ Link verweist auf die PDF-Version; Kapitel 12: Seite 271-294.

Prinzip und Motivation

Viele Nachrichtensignale sind analog und damit gleichzeitig zeitkontinuierlich und wertkontinuierlich. Soll ein solches Analogsignal mittels eines Digitalsystems übertragen werden, so sind folgende Vorverarbeitungsschritte erforderlich:

die $\text{Abtastung}$ des Nachrichtensignals $x(t)$, die zweckmäßigerweise – aber nicht notwendigerweise – zu äquidistanten Zeitpunkten erfolgt ⇒ $\text{Zeitdiskretisierung}$,
die $\text{Quantisierung}$ der Abtastwerte, um so die Anzahl $M$ der möglichen Werte auf einen endlichen Wert zu begrenzen ⇒ $\text{Wertdiskretisierung}$.

Die Quantisierung wird erst im Kapitel Pulscodemodulation des Buches „Modulationsverfahren” im Detail behandelt.

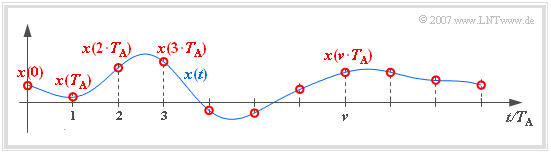
Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur:

Zur Zeitdiskretisierung des zeitkontinuierlichen Signals $x(t)$

Das zeitkontinuierliche Signal sei $x(t)$.
Das in äquidistanten Abständen $T_{\rm A}$ abgetastete Signal sei $x_{\rm A}(t)$.
Die Laufvariable $\nu$ der Abtastung sei ganzzahlig: :$$\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} .$$
Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) = 0$.

Zu den äquidistanten Abtastzeitpunkten ergibt sich mit der Konstanten $K$:

$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$

Die Konstante hängt von der Art der Zeitdiskretisierung ab. Hier: $K = 1$.

Zeitbereichsdarstellung

$\text{Definition:}$ Im gesamten $\rm LNTwww$ soll unter $\text{Abtastung}$ die Multiplikation des zeitkontinuierlichen Signals $x(t)$ mit dem Diracpuls $p_{\delta}(t)$ verstanden werden:

$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$

Anzumerken ist, dass in der Literatur auch andere Beschreibungsformen gefunden werden. Den Autoren erscheint jedoch die hier gewählte Form im Hinblick auf die Spektraldarstellung und die Herleitung der Diskreten Fouriertransformation $\rm (DFT)$ am besten geeignet.

$\text{Definition:}$ Der $\text{Diracpuls}$ (im Zeitbereich) besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$:

$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

Aufgrund dieser Definition ergeben sich für das abgetastete Signal folgende Eigenschaften:

Das abgetastete Signal zum betrachteten Zeitpunkt $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$.
Da die Diracfunktion $\delta (t)$ zur Zeit $t = 0$ unendlich ist, sind eigentlich alle Signalwerte $x_{\rm A}(\nu \cdot T_{\rm A})$ ebenfalls unendlich groß.
Somit ist auch der auf der letzten Seite eingeführte Faktor $K$ eigentlich unendlich groß.
Zwei Abtastwerte $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ und $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ unterscheiden sich jedoch im gleichen Verhältnis wie die Signalwerte $x(\nu_1 \cdot T_{\rm A})$ und $x(\nu_2 \cdot T_{\rm A})$.
Die Abtastwerte von $x(t)$ erscheinen in den Impulsgewichten der Diracfunktionen:

$$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

Die zusätzliche Multiplikation mit $T_{\rm A}$ ist erforderlich, damit $x(t)$ und $x_{\rm A}(t)$ gleiche Einheit besitzen. Beachten Sie, dass $\delta (t)$ selbst die Einheit „1/s” aufweist.

Die folgenden Seiten werden zeigen, dass diese gewöhnungsbedürftigen Gleichungen durchaus zu sinnvollen Ergebnissen führen, wenn man sie konsequent anwendet.

Diracpuls im Zeit- und im Frequenzbereich

$\text{Satz:}$ Entwickelt man den $\text{Diracpuls}$ in eine Fourierreihe und transformiert diese unter Anwendung des Verschiebungssatzes in den Frequenzbereich, so ergibt sich folgende Korrespondenz:

$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$$

Hierbei gibt $f_{\rm A} = 1/T_{\rm A}$ den Abstand zweier benachbarter Diraclinien im Frequenzbereich an.

$\text{Beweis:}$ Die Herleitung der hier angegebenen Spektralfunktion $P_{\delta}(f)$ geschieht in mehreren Schritten:

(1) Da $p_{\delta}(t)$ periodisch mit dem konstanten Abstand $T_{\rm A}$ zwischen zwei Diraclinien ist, kann die (komplexe) Fourierreihendarstellung angewendet werden:

$$p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} D_{\mu} \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} } \hspace{0.3cm}{\rm mit}\hspace{0.3cm} D_{\mu} = \frac{1}{T_{\rm A} } \cdot \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}p_{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$

(2) Im Bereich von $–T_{\rm A}/2$ bis $+T_{\rm A}/2$ gilt für den Diracpuls im Zeitbereich: $p_{\delta}(t) = T_{\rm A} \cdot \delta(t)$. Damit kann man für die komplexen Fourierkoeffizienten schreiben:

$$D_{\mu} = \int_{-T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2 \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm} \cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.1cm} {\rm d}t\hspace{0.05cm}.$$

(3) Unter Berücksichtigung der Tatsache, dass für $t \neq 0$ der Diracimpuls Null ist und für $t = 0$ der komplexe Drehfaktor gleich $1$, gilt weiter:

$$D_{\mu} = \int_{- T_{\rm A}/2 }^{+T_{\rm A}/2}{\delta}(t) \hspace{0.1cm} {\rm d}t = 1\hspace{0.5cm}{\Rightarrow}\hspace{0.5cm} p_{\delta}(t) = \sum_{\mu = - \infty }^{+\infty} {\rm e}^{ {\rm j} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm}t/T_{\rm A} }\hspace{0.05cm}. $$

(4) Der Verschiebungssatz im Frequenzbereich lautet mit $f_{\rm A} = 1/T_{\rm A}$:

$${\rm e}^{ {\rm j} \hspace{0.05cm} \hspace{0.05cm} \cdot 2 \hspace{0.05cm} \pi \hspace{0.05cm}\cdot \hspace{0.05cm}\mu \hspace{0.05cm}\cdot \hspace{0.05cm} f_{\rm A}\hspace{0.05cm}\cdot \hspace{0.05cm}t}\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

(5) Wendet man das Ergebnis auf jeden einzelnen Summanden an, so erhält man schließlich:

$$P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

q.e.d.

Das Ergebnis besagt:

Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$.
Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$.
$P_{\delta}(f)$ besteht ebenfalls aus unendlich vielen Diracimpulsen, nun aber im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$.
Die Abstände der Diraclinien in der Zeit– und Frequenzbereichsdarstellung folgen demnach dem Reziprozitätsgesetz:

$$T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$$

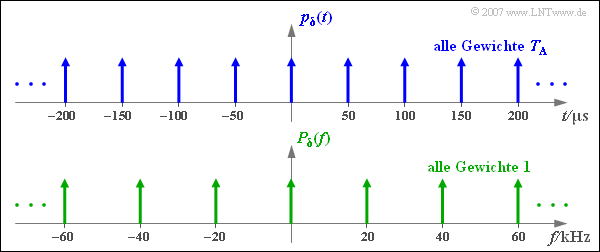
Diracpuls im Zeit- und Frequenzbereich

$\text{Beispiel 1:}$ Die Grafik verdeutlicht die obigen Aussagen für

$T_{\rm A} = 50\,{\rm µs}$,
$f_{\rm A} = 1/T_{\rm A} = 20\,\text{kHz}$ .

Man erkennt aus dieser Skizze auch die unterschiedlichen Impulsgewichte von $p_{\delta}(t)$ und $P_{\delta}(f)$.

Frequenzbereichsdarstellung

Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des Faltungssatzes. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht:

$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$

Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie:

$$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich:

$$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

$\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer $\text{periodischen Fortsetzung}$ von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$.

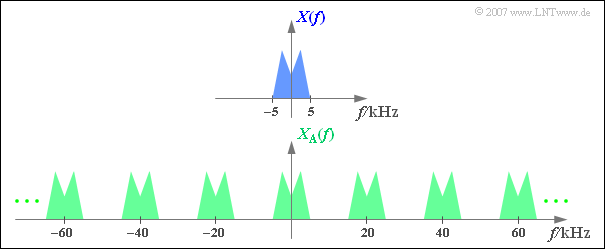
$\text{Beispiel 2:}$ Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$, das Frequenzen bis $5 \text{ kHz}$ beinhaltet.

Spektrum des abgetasteten Signals

Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$, also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$.

Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile.
Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.

Signalrekonstruktion

Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden.

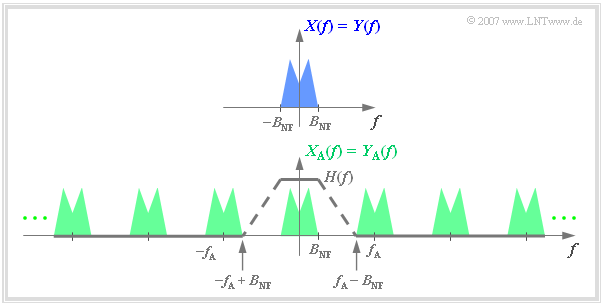
Signalabtastung und Signalrekonstruktion

Betrachten wir zum Beispiel das nebenstehende System:

Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet.
Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor.
Die Frage ist nun, wie der Block Signalrekonstruktion zu gestalten ist, damit auch $y(t) = x(t)$ gilt.

Frequenzbereichsdarstellung der Signalrekonstruktion

Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet:

Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch einen Tiefpass mit dem Frequenzgang $H(f)$, der

die tiefen Frequenzen unverfälscht durchlässt:

$$H(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$$

die hohen Frequenzen vollständig unterdrückt:

$$H(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$$

Weiter ist aus der Grafik zu erkennen, dass der Frequenzgang $H(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann, solange die beiden oben genannten Bedingungen erfüllt sind,

beispielsweise linear abfallend (gestrichelter Verlauf)
oder auch rechteckförmig.

Das Abtasttheorem

Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde.

Aus der Grafik der letzten Seite erkennt man, dass folgende Bedingung erfüllt sein muss:

$$f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$$

$\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$, so kann dieses aus seinem abgetasteten Signal nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist:

$$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$$

Für den Abstand zweier Abtastwerte muss demnach gelten:

$$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$$

Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen,

so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten
ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden.

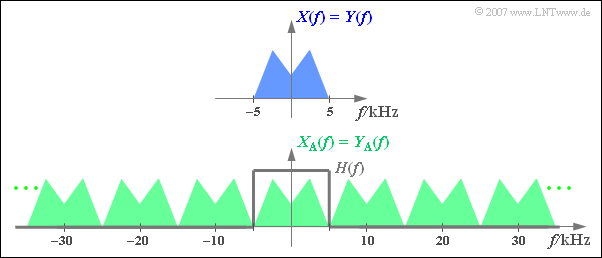
$\text{Beispiel 3:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$.

Abtasttheorem im Frequenzbereich

Zusätzlich eingezeichnet ist der Frequenzgang $H(f)$ des rechteckförmigen Tiefpasses zur Signalrekonstruktion, dessen Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss.

Mit jedem anderen $f_{\rm G}$–Wert ergäbe sich $Y(f) \neq X(f)$.
Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$–Anteile.
Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$.

Wäre die Abtastung am Sender mit der Abtastrate $f_{\rm A} < 10\,\text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \,{\rm µ s}$, so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.

Hinweis: Zu der hier behandelten Thematik gibt es ein interaktives Applet: Abtastung analoger Signale und Signalrekonstruktion

Aufgaben zum Kapitel

Aufgabe 5.1: Zum Abtasttheorem

Aufgabe 5.1Z: Abtastung harmonischer Schwingungen