Aufgabe 4.4Z: Störabstand bei PCM
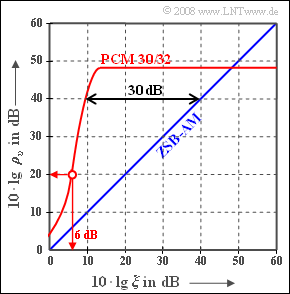
Die Grafik zeigt den Sinken–Störabstand $10 · lg ρ_υ$ bei Pulscodemodulation (PCM) im Vergleich zur analogen Zweiseitenband–Amplitudenmodulation, abgekürzt mit ZSB–AM. Für letztere gilt $ρ_υ = ξ$, wobei $$\xi = \frac{\alpha^2 \cdot P_{\rm S}}{N_0 \cdot f_{\rm N}} \hspace{0.05cm}.$$ folgende Systemparameter zusammenfasst:
- den frequenzunabhängigen Dämpfungsfaktor $α$ des Übertragungskanals,
- die Leistung $P_S$ des Sendsignals $s(t)$, auch kurz Sendeleistung genannt,
- die Nachrichtenfrequenz $f_N$ (Bandbreite) des cosinusförmigen Quellensignals $q(t)$,
- die Rauschleistungsdichte $N_0$ des AWGN–Rauschens.
Für das PCM–System wurde auf der Seite Einfluss von Übertragungsfehlern (4) folgende Näherung für das Sinken–SNR angegeben, die auch Bitfehler aufgrund des AWGN–Rauschens berücksichtigt: $$ \rho_{\upsilon}= \frac{1}{ 2^{-2N } + 4 \cdot p_{\rm B}} \hspace{0.05cm}.$$ Hierbei bezeichnet $N$ die Anzahl der Bit pro Abtastwert und pB die Bitfehlerwahrscheinlichkeit. Da $ξ$ bei digitaler Modulation auch als die Signalenergie pro Bit bezogen auf die Rauschleistungsdichte ($E_B/N_0$) interpretiert werden kann, gilt mit dem komplementären Gaußschen Fehlersignal $Q(x)$ näherungsweise: $$ p_{\rm B}= {\rm Q} \left ( \sqrt{2 \xi }\right ) \hspace{0.05cm}.$$ Hinweis: Die Aufgabe bezieht sich auf das Kapitel 4.1 Bei der hier betrachteten PCM handelt es sich um die PCM 30/32, deren Systemparameter zum Beispiel in der Aufgabe A4.1 angegeben sind.
Fragebogen
Musterlösung