Differentielle Entropie

Inhaltsverzeichnis

1 # ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #
2 Eigenschaften wertkontinuierlicher Zufallsgrößen
3 Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung
4 Definition und Eigenschaften der differentiellen Entropie
5 Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen
6 Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen
7 Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung
8 Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung
9 Aufgaben zum Kapitel

# ÜBERBLICK ZUM VIERTEN HAUPTKAPITEL #

Im letzten Kapitel dieses Buches werden die bisher für den wertdiskreten Fall definierten informationstheoretischen Größen derart adaptiert, dass sie auch für wertkontinuierliche Zufallsgrößen angewandt werden können.

Aus der Entropie $H(X)$ für die wertdiskrete Zufallsgröße $X$ wird so zum Beispiel im wertkontinuierlichen Fall die differentielle Entropie $h(X)$.
Während $H(X)$ die „Unsicherheit” hinsichtlich der diskreten Zufallsgröße $X$ angibt, kann die differentielle Entropie $h(X)$ einer kontinuierlichen Zufallsgröße nicht in gleicher Weise interpretiert werden.

Viele der im dritten Kapitel „Information zwischen zwei wertdiskreten Zufallsgrößen ⇒ siehe Inhaltsverzeichnis für die herkömmliche Entropie hergeleiteten Zusammenhänge gelten auch für die differentielle Entropie. So kann auch für wertkontinuierliche Zufallsgrößen $X$ und $Y$ die differentielle Verbundentropie $h(XY)$ angegeben werden und ebenso die beiden bedingten differentiellen Entropien $h(Y|X)$ und $h(X|Y)$.

Im Einzelnen werden in diesem Hauptkapitel behandelt:

die Besonderheiten wertkontinuierlicher Zufallsgrößen,
die Definition und Berechnung der differentiellen Entropie sowie deren Eigenschaften,
die Transinformation zwischen zwei wertkontinuierlichen Zufallsgrößen,
die Kapazität des AWGN– Kanals und mehrerer solcher paralleler Gaußkanäle,
das Kanalcodierungstheorem, eines der Highlights der Shannonschen Informationstheorie,
die Kanalkapazität für wertdiskrete Eingangssinale (BPSK, QPSK).

Eigenschaften wertkontinuierlicher Zufallsgrößen

Bisher wurden stets wertdiskrete Zufallsgrößen der Form $X = \{x_1, x_2, \hspace{0.05cm}\text{...}\hspace{0.05cm} , x_μ, \text{...} , x_M\}$ betrachtet, die aus informationstheoretischer Sicht vollständig durch ihre Wahrscheinlichkeitsfunktion (englisch: Probability Mass Function, PMF) $P_X(X)$ charakterisiert werden:

$$P_X(X) = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_{\mu},\hspace{0.05cm} \text{...}\hspace{0.15cm}, p_M \hspace{0.1cm}\big ] \hspace{0.3cm}{\rm mit} \hspace{0.3cm} p_{\mu}= P_X(x_{\mu})= {\rm Pr}( X = x_{\mu}) \hspace{0.05cm}.$$

Eine wertkontinuierliche Zufallsgröße kann dagegen – zumindest in endlichen Intervallen – jeden beliebigen Wert annehmen:

Aufgrund des nicht abzählbaren Wertevorrats ist in diesem Fall die Beschreibung durch eine Wahrscheinlichkeitsfunktion nicht möglich oder zumindest nicht sinnvoll:
Es ergäbe sich nämlich $M \to ∞$ sowie $p_1 \to 0$, $p_2 \to 0$, usw.

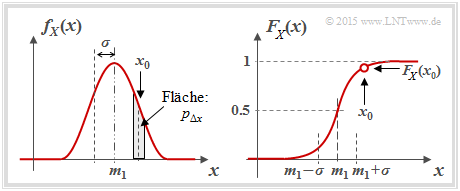
WDF und VTF einer wertkontinuierlichen Zufallsgröße

Man verwendet zur Beschreibung wertkontinuierlicher Zufallsgrößen gemäß den Definitionen im Buch Stochastische Signaltheorie gleichermaßen (beachten Sie die Einträge in der Grafik):

die Wahrscheinlichkeitsdichtefunktion (WDF, englisch: Probability Density Function, PDF):

$$f_X(x_0)= \lim_{{\rm \Delta} x\to \rm 0}\frac{p_{{\rm \Delta} x}}{{\rm \Delta} x} = \lim_{{\rm \Delta} x\to \rm 0}\frac{{\rm Pr} \{ x_0- {\rm \Delta} x/\rm 2 \le \it X \le x_{\rm 0} +{\rm \Delta} x/\rm 2\}}{{\rm \Delta} x};$$

In Worten: Der WDF–Wert bei $x_0$ gibt die Wahrscheinlichkeit $p_{Δx}$ an, dass $X$ in einem (unendlich kleinen) Intervall der Breite $Δx$ um $x_0$ liegt, dividiert durch $Δx$;

den Mittelwert (Moment erster Ordnung, englisch: Mean Value bzw. Expectation Value):

$$m_1 = {\rm E}\big[ X \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} x \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$

die Varianz (Zentralmoment zweiter Ordnung, englisch: Variance):

$$\sigma^2 = {\rm E}\big[(X- m_1 )^2 \big]= \int_{-\infty}^{+\infty} \hspace{-0.1cm} (x- m_1 )^2 \cdot f_X(x- m_1 ) \hspace{0.1cm}{\rm d}x \hspace{0.05cm};$$

die Verteilungsfunktion (VTF, englisch: Cumulative Distribution Function, CDF):

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

Beachten Sie, dass sowohl die WDF–Fläche als auch der VTF–Endwert stets gleich $1$ sind.

$\text{Nomenklaturhinweise zu WDF und VTF:}$

Wir verwenden in diesem Kapitel für eine Wahrscheinlichkeitsdichtefunktion die in der Literatur häufig verwendete Darstellungsform $f_X(x)$, wobei gilt:

$X$ bezeichnet die (wertdiskrete oder wertkontinuierliche) Zufallsgröße,
$x$ ist eine mögliche Realisierung von $X$ ⇒ $x ∈ X$.

Entsprechend bezeichnen wir die Verteilungsfunktion (VTF) der Zufallsgröße $X$ mit $F_X(x)$ entsprechend folgender Definition:

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

In anderen $\rm LNTwww$–Büchern schreiben wir oft, um nicht für eine Variable zwei Zeichen zu verbrauchen:

Für die WDF $f_x(x)$ ⇒ keine Unterscheidung zwischen Zufallsgröße und Realisiering,
für die VTF $F_x(r) = {\rm Pr}(x ≤ r)$ ⇒ hier benötigt man auf jeden Fall eine zweite Variable.

Wir bitten, diese formale Ungenauigkeit zu entschuldigen.

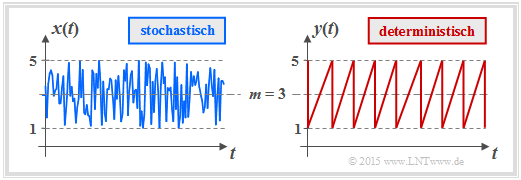
$\text{Beispiel 1:}$ Wir betrachten nun mit der Gleichverteilung einen wichtigen Sonderfall.

Die Grafik zeigt den Verlauf zweier gleichverteilter Größen, die alle Werte zwischen $1$ und $5$ (Mittelwert $m_1 = 3$) mit gleicher Wahrscheinlichkeit annehmen können.
Links ist das Ergebnis eines Zufallsprozesses dargestellt, rechts ein deterministisches Signal („Sägezahn”) mit gleicher Amplitudenverteilung.

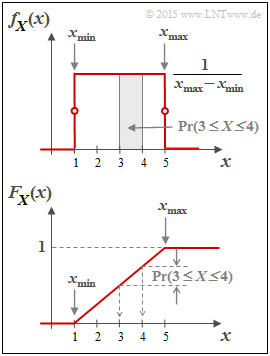
Zwei Analogsignale als Beispiele für wertkontinuierliche Zufallsgrößen

WDF und VTF einer gleichverteilten Zufallsgröße

Die Wahrscheinlichkeitsdichtefunktion der Gleichverteilung hat den in der zweiten Grafik oben skizzierten Verlauf:

$$f_X(x) = \left\{ \begin{array}{c} \hspace{0.25cm}(x_{\rm max} - x_{\rm min})^{-1} \\ 1/2 \cdot (x_{\rm max} - x_{\rm min})^{-1} \\ \hspace{0.25cm} 0 \\ \end{array} \right. \begin{array}{*{20}c} {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ {\rm{f\ddot{u}r} } \\ \end{array} \begin{array}{*{20}l} {x_{\rm min} < x < x_{\rm max},} \\ x ={x_{\rm min} \hspace{0.1cm}{\rm und}\hspace{0.1cm}x = x_{\rm max},} \\ x > x_{\rm max}. \\ \end{array}$$

Es ergeben sich hier für den Mittelwert $m_1$ = ${\rm E}[X]$ und die Varianz $σ_2$ = ${\rm E}[(X – m_1)^2]$ folgende Gleichungen:

$$m_1 = \frac{x_{\rm max} + x_{\rm min} }{2}\hspace{0.05cm}, \hspace{0.5cm} \sigma^2 = \frac{(x_{\rm max} - x_{\rm min})^2}{12}\hspace{0.05cm}.$$

Unten dargestellt ist die Verteilungsfunktion (VTF):

$$F_X(x) = \int_{-\infty}^{x} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(X \le x)\hspace{0.05cm}.$$

Diese ist für $x ≤ x_{\rm min}$ identisch $0$, steigt danach linear an und erreicht bei $x = x_{\rm max}$ den VTF–Endwert $1$.
Die Wahrscheinlichkeit, dass die Zufallgröße $X$ einen Wert zwischen $3$ und $4$ annimmt, kann sowohl aus der WDF als auch aus der VTF ermittelt werden:

$${\rm Pr}(3 \le X \le 4) = \int_{3}^{4} \hspace{-0.1cm}f_X(\xi) \hspace{0.1cm}{\rm d}\xi = 0.25\hspace{0.05cm}\hspace{0.05cm},$$

$${\rm Pr}(3 \le X \le 4) = F_X(4) - F_X(3) = 0.25\hspace{0.05cm}.$$

Weiterhin ist zu beachten:

Das Ergebnis $X = 0$ ist bei dieser Zufallsgröße ausgeschlossen ⇒ ${\rm Pr}(X = 0) = 0$.
Das Ergebnis $X = 4$ ist dagegen durchaus möglich. Trotzdem gilt auch hier ${\rm Pr}(X = 4) = 0$.

Entropie wertkontinuierlicher Zufallsgrößen nach Quantisierung

Wir betrachten nun eine wertkontinuierliche Zufallsgröße $X$ im Bereich von $0 \le x \le 1$.

Wir quantisieren die kontinuierliche Zufallsgröße $X$, um die bisherige Entropieberechnung weiter anwenden zu können. Die so entstehende diskrete (quantisierte) Größe nennen wir $Z$.
Die Quantisierungsstufenzahl sei $M$, so dass jedes Quantisierungsintervall $μ$ bei der vorliegenden WDF die Breite ${\it Δ} = 1/M$ aufweist. Die Intervallmitten bezeichnen wir mit $x_μ$.
Die Wahrscheinlichkeit $p_μ = {\rm Pr}(Z = z_μ)$ bezüglich $Z$ ist gleich der Wahrscheinlichkeit, dass die kontinuierliche Zufallsgröße $X$ einen Wert zwischen $x_μ – {\it Δ}/2$ und $x_μ + {\it Δ}/2$ besitzt.
Zunächst setzen wir $M = 2$ und verdoppeln anschließend $M$ in jeder Iteration. Dadurch wird die Quantisierung zunehmend feiner. Im $n$–ten Versuch gilt dann $M = 2^n$ und ${\it Δ} =2^{–n}$.

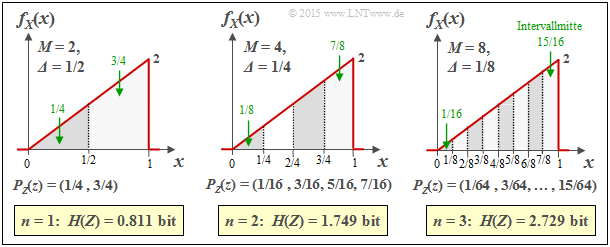
Entropiebestimmung der Dreieck–WDF nach Quantisierung

$\text{Beispiel 2:}$ Die Grafik zeigt die Ergebnisse der ersten drei Versuche für eine dreieckförmige WDF (zwischen $0$ und $1$):

$n = 1 \ ⇒ \ M = 2 \ ⇒ \ {\it Δ} = 1/2\text{:}$

$$H(Z) = 0.811\ \rm bit,$$

$n = 2 \ ⇒ \ M = 4 \ ⇒ \ {\it Δ} = 1/4\text{:}$

$$H(Z) = 1.749\ \rm bit,$$

$n = 3 \ ⇒ \ M = 8 \ ⇒ \ {\it Δ} = 1/8\text{:}$

$$H(Z) = 2.729\ \rm bit.$$

Zudem können der Grafik noch folgende Größen entnommen werden, zum Beispiel für ${\it Δ} = 1/8$:

Die Intervallmitten liegen bei $x_1 = 1/16,\ x_2 = 3/16,\text{ ...} \ ,\ x_8 = 15/16 \ ⇒ \ x_μ = {\it Δ} · (μ – 1/2)$.
Die Intervallflächen ergeben sich zu $p_μ = {\it Δ} · f_X(x_μ) \ ⇒ \ p_8 = 1/8 · (7/8+1)/2 = 15/64$.
Damit erhält man $P_Z(Z) = (1/64, \ 3/64, \ 5/64, \ 7/64, \ 9/64, \ 11/64, \ 13/64, \ 15/64)$.

$\text{Fazit:}$ Die Ergebnisse dieses Experiments interpretieren wir wie folgt:

Die Entropie $H(Z)$ nimmt mit steigendem $M$ immer mehr zu.
Der Grenzwert von $H(Z)$ für $M \to ∞ \ ⇒ \ {\it Δ} → 0$ ist unendlich.
Damit ist auch die Entropie $H(X)$ der wertkontinuierlichen Zufallsgröße $X$ unendlich groß.
Daraus folgt: Die bisherige Entropie–Definition versagt hier.

Zur Verifizierung unseres empirischen Ergebnisses gehen wir von folgender Gleichung aus:

$$H(Z) = \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} p_{\mu} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\mu}}= \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} {\it \Delta} \cdot f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{{\it \Delta} \cdot f_X(x_{\mu} )}\hspace{0.05cm}.$$

Wir spalten nun $H(Z) = S_1 + S_2$ in zwei Summen auf:

$$\begin{align*}S_1 & = {\rm log}_2 \hspace{0.1cm} \frac{1}{\it \Delta} \cdot \hspace{0.2cm} \sum_{\mu = 1}^{M} \hspace{0.02cm} {\it \Delta} \cdot f_X(x_{\mu} ) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.05cm},\\ S_2 & = \hspace{0.05cm} \sum_{\mu = 1}^{M} \hspace{0.2cm} f_X(x_{\mu} ) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x_{\mu} ) } \cdot {\it \Delta} \hspace{0.2cm}\approx \hspace{0.2cm} \int_{0}^{1} \hspace{0.05cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$

Die Näherung $S_1 ≈ -\log_2 {\it Δ}$ gilt exakt nur im Grenzfall ${\it Δ} → 0$. Die angegebene Näherung für $S_2$ gilt ebenfalls nur für kleine ${\it Δ} → {\rm d}x$, so dass man die Summe durch das Integral ersetzen kann.

$\text{Verallgemeinerung:}$ Nähert man die wertkontinuierliche Zufallsgröße $X$ mit der WDF $f_X(x)$ durch eine wertdiskrete Zufallsgröße $Z$ an, indem man eine (feine) Quantisierung mit der Intervallbreite ${\it Δ}$ durchführt, so erhält man für die Entropie der Zufallsgröße $Z$:

$$H(Z) \approx - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm}+ \hspace{-0.35cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x = - {\rm log}_2 \hspace{0.1cm}{\it \Delta} \hspace{0.2cm} + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$

Das Integral beschreibt die differentielle Entropie $h(X)$ der wertkontinuierlichen Zufallsgröße $X$. Für den Sonderfall ${\it Δ} = 1/M = 2^{-n}$ kann die obige Gleichung auch wie folgt geschrieben werden:

$$H(Z) = n + h(X) \hspace{0.5cm}\big [{\rm in \hspace{0.15cm}bit}\big ] \hspace{0.05cm}.$$

Im Grenzfall ${\it Δ} → 0 \ ⇒ \ M → ∞ ⇒ n → ∞$ ist auch die Entropie der wertkontinuierlichen Zufallsgröße unendlich groß: $H(X) → ∞$.
Auch bei kleinerem $n$ stellt diese Gleichung lediglich eine Näherung für $H(Z)$ dar, wobei die differentielle Entropie $h(X)$ der wertkontinuierlichen Größe als Korrekturfaktor dient.

$\text{Beispiel 3:}$ Wir betrachten wie im $\text{Beispiel 2}$ eine Dreieck–WDF (zwischen $0$ und $1$). Deren differentielle Entropie ergibt sich, wie in der Aufgabe 4.2 berechnet, zu $h(X) = \hspace{0.05cm}-0.279 \ \rm bit$ .

In der Tabelle ist die Entropie $H(Z)$ der mit $n$ Bit quantisierten Größe $Z$ angegeben.
Man erkennt bereits für $n = 3$ eine gute Übereinstimmung zwischen der Näherung (untere Zeile) und der exakten Berechnung (Zeile 2).

Entropie der Dreieck–WDF nach Quantisierung

Definition und Eigenschaften der differentiellen Entropie

$\text{Verallgemeinerung:}$ Die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße $X$ lautet mit der Wahrscheinlichkeitsdichtefunktion $f_X(x)$:

$$h(X) = \hspace{0.1cm} - \hspace{-0.45cm} \int\limits_{\text{supp}(f_X)} \hspace{-0.35cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \big[ f_X(x) \big] \hspace{0.1cm}{\rm d}x \hspace{0.6cm}{\rm mit}\hspace{0.6cm} {\rm supp}(f_X) = \{ x\text{:} \ f_X(x) > 0 \} \hspace{0.05cm}.$$

Hinzugefügt werden muss jeweils eine Pseudo–Einheit:

„nat” bei Verwendung von „ln” ⇒ natürlicher Logarithmus,
„bit” bei Verwendung von „log₂” ⇒ Logarithmus dualis.

Während für die (herkömmliche) Entropie einer wertdiskreten Zufallsgröße $X$ stets $H(X) ≥ 0$ gilt, kann die differentielle Entropie $h(X)$ einer wertkontinuierlichen Zufallsgröße auch negativ sein. Daraus ist bereits ersichtlich, dass $h(X)$ im Gegensatz zu $H(X)$ nicht als „Unsicherheit” interpretiert werden kann.

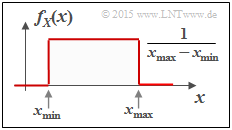
WDF einer gleichverteilten Zufallsgröße

$\text{Beispiel 4:}$ Die Grafik zeigt die Wahrscheinlichkeitsdichte einer zwischen $x_{\rm min}$ und $x_{\rm max}$ gleichverteilten Zufallsgröße $X$. Für deren differentielle Entropie erhält man in „nat”:

$$\begin{align*}h(X) & = - \hspace{-0.18cm}\int\limits_{x_{\rm min} }^{x_{\rm max} } \hspace{-0.28cm} \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \cdot {\rm ln} \hspace{0.1cm}\big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \hspace{0.1cm}{\rm d}x \\ & = {\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} }\big ] \cdot \big [ \frac{1}{x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big ]_{x_{\rm min} }^{x_{\rm max} }={\rm ln} \hspace{0.1cm} \big[ {x_{\rm max}\hspace{-0.05cm} - \hspace{-0.05cm}x_{\rm min} } \big]\hspace{0.05cm}.\end{align*} $$

Die Gleichung für die differentielle Entropie in „bit” lautet: $h(X) = \log_2 \big[x_{\rm max} – x_{ \rm min} \big]$.

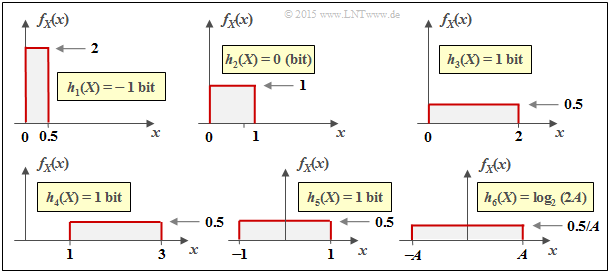
Die untere Grafik zeigt anhand einiger Beispiele die numerische Auswertung des obigen Ergebnisses.

$h(X)$ für verschiedene rechteckförmige Dichtefunktionen

$\text{Interpretation:}$ Aus den sechs Skizzen im letzten Beispiel lassen sich wichtige Eigenschaften der differentiellen Entropie $h(X)$ ablesen:

Die differentielle Entropie wird durch eine WDF–Verschiebung (um $k$) nicht verändert:

$$h(X + k) = h(X) \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_3(X) = h_4(X) = h_5(X) \hspace{0.05cm}.$$

$h(X)$ ändert sich durch Stauchung/Spreizung der WDF um den Faktor $k ≠ 0$ wie folgt:

$$h( k\hspace{-0.05cm} \cdot \hspace{-0.05cm}X) = h(X) + {\rm log}_2 \hspace{0.05cm} \vert k \vert \hspace{0.2cm}\Rightarrow \hspace{0.2cm} \text{Beispielsweise gilt} \ \ h_6(X) = h_5(AX) = h_5(X) + {\rm log}_2 \hspace{0.05cm} (A) = {\rm log}_2 \hspace{0.05cm} (2A) \hspace{0.05cm}.$$

Des Weiteren gelten viele der im Kapitel Verschiedene Entropien zweidimensionaler Zufallsgrößen für den wertdiskreten Fall hergeleitete Gleichungen auch für wertkontinuierliche Zufallsgrößen.

Aus der folgenden Zusammenstellung erkennt man, dass oft nur das „$H$” durch ein „$h$” sowie die Wahrscheinlichkeitsfunktion (englische Abkürzung: PMF) durch die entsprechende Wahrscheinlichkeitsdichtefunktion (WDF bzw. PDF) zu ersetzen ist.

Bedingte differentielle Entropie (englisch: Conditional Differential Entropy):

$$H(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm}h(X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y) = {\rm E} \hspace{-0.1cm}\left [ {\rm log} \hspace{0.1cm}\frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (X \hspace{-0.05cm}\mid \hspace{-0.05cm} Y)}\right ]=\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{f_{\hspace{0.03cm}X \mid \hspace{0.03cm} Y} (x \hspace{-0.05cm}\mid \hspace{-0.05cm} y)} \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

Differentielle Verbundentropie (englisch: Joint Differential Entropy):

$$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] =\hspace{-0.04cm} \sum_{(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{XY}\hspace{-0.08cm})} \hspace{-0.8cm} P_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ P_{XY}(x, y)} \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm}h(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{f_{XY}(X, Y)}\right ] =\hspace{0.2cm} \int \hspace{-0.9cm} \int\limits_{\hspace{-0.04cm}(x, y) \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}f_{XY}\hspace{-0.08cm})} \hspace{-0.6cm} f_{XY}(x, y) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_{XY}(x, y) } \hspace{0.15cm}{\rm d}x\hspace{0.15cm}{\rm d}y\hspace{0.05cm}.$$

Kettenregel der differentiellen Entropie:

$$H(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} H(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} H(X_i) \hspace{0.05cm}$$

$$\Rightarrow \hspace{0.3cm} h(X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_n) =\sum_{i = 1}^{n} h(X_i | X_1\hspace{0.05cm}X_2\hspace{0.05cm}\text{...} \hspace{0.1cm}X_{i-1}) \le \sum_{i = 1}^{n} h(X_i) \hspace{0.05cm}.$$

Kullback–Leibler–Distanz zwischen den Zufallsgrößen $X$ und $Y$:

$$D(P_X \hspace{0.05cm} || \hspace{0.05cm}P_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{P_X(X)}{P_Y(X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp} \hspace{0.03cm}(\hspace{-0.03cm}P_{X})\hspace{-0.8cm}} P_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{P_X(x)}{P_Y(x)} \ge 0$$

$$\Rightarrow \hspace{0.3cm}D(f_X \hspace{0.05cm} || \hspace{0.05cm}f_Y) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{f_X(X)}{f_Y(X)}\right ] \hspace{0.2cm}= \hspace{-0.4cm}\int\limits_{x \hspace{0.1cm}\in \hspace{0.1cm}{\rm supp}\hspace{0.03cm}(\hspace{-0.03cm}f_{X}\hspace{-0.08cm})} \hspace{-0.4cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{f_X(x)}{f_Y(x)} \hspace{0.15cm}{\rm d}x \ge 0 \hspace{0.05cm}.$$

Differentielle Entropie einiger spitzenwertbegrenzter Zufallsgrößen

Die Tabelle zeigt die Ergebnisse für drei beispielhafte Wahrscheinlichkeitsdichtefunktionen $f_X(x)$. Diese sind alle spitzenwertbegrenzt, das heißt, es gilt jeweils $|X| ≤ A$.
Bei Spitzenwertbegrenzung kann man die differentielle Entropie stets wie folgt darstellen:

Differentielle Entropie spitzenwertbegrenzter Zufallsgrößen

$$h(X) = {\rm log}\,\, ({\it \Gamma}_{\rm A} \cdot A).$$

Das Argument ${\it \Gamma}_A · A$ ist unabhängig davon, welchen Logarithmus man verwendet. Anzufügen ist

bei Verwendung von $\ln$ ist die Pseudo–Einheit „nat”,
bei Verwendung von $\log_2$ ist die Pseudo–Einheit „bit”.

$\text{Theorem:}$ Unter der Nebenbedingung Spitzenwertbegrenzung (englisch: Peak Constraint) ⇒ also WDF $f_X(x) = 0$ für $ \vert x \vert > A$ – führt die Gleichverteilung zur maximalen differentiellen Entropie:

$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} (2A)\hspace{0.05cm}.$$

Hier ist die geeignete Kenngröße ${\it \Gamma}_{\rm A} = 2$ maximal. Sie finden den Beweis am Ende dieses Kapitels.

Das Theorem bedeutet gleichzeitig, dass bei jeder anderen spitzenwertbegrenzten WDF (außer der Gleichverteilung) der Kennparameter ${\it \Gamma}_{\rm A} < 2$ ist.

Für die symmetrische Dreieckverteilung ergibt sich nach obiger Tabelle ${\it \Gamma}_{\rm A} = \sqrt{\rm e} ≈ 1.649$.
Beim einseitigen Dreieck (zwischen $0$ und $A$) ist demgegenüber ${\it \Gamma}_{\rm A}$ nur halb so groß.
Auch für jedes andere Dreieck (Breite $A$, Spitze beliebig zwischen $0$ und $A$) gilt ${\it \Gamma}_{\rm A} ≈ 0.824$.

Die jeweils zweite $h(X)$–Angabe und die Kenngröße ${\it \Gamma}_{\rm L}$ eignet sich dagegen für den Vergleich von Zufallsgrößen bei Leistungsbegrenzung, der im nächsten Abschnitt behandelt wird. Unter dieser Nebenbedingung ist zum Beispiel die symmetrische Dreieckverteilung $({\it \Gamma}_{\rm L} ≈ 16.31)$ besser als die Gleichverteilung ${\it \Gamma}_{\rm L} = 12)$.

Differentielle Entropie einiger leistungsbegrenzter Zufallsgrößen

Die differentiellen Entropien $h(X)$ für drei beispielhafte Dichtefunktionen $f_X(x)$ ohne Begrenzung, die alle die gleiche Varianz $σ^2 = {\rm E}\big[|X -m_x|^2 \big]$ und damit gleiche Streuung $σ$ aufweisen, sind der folgenden Tabelle zu entnehmen:

Differentielle Entropie leistungsbegrenzter Zufallsgrößen

die Gaußverteilung,
die Laplaceverteilung ⇒ eine zweiseitige Exponentialverteilung,
die (einseitige) Exponentialverteilung.

Die differentielle Entropie lässt sich bei allen diesen Beispielen als

$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm L} \cdot \sigma^2)$$

darstellen. Das Ergebnis unterscheidet sich nur durch

die Pseudo–Einheit „nat” bei Verwendung von $\ln$
bzw. „bit” bei Verwendung von $\log_2$.

$\text{Theorem:}$ Unter der Nebenbedingung der Leistungsbegrenzung (englisch: Power Constraint) führt die Gaußverteilung

$$f_X(x) = \frac{1}{\sqrt{2\pi \sigma^2} } \cdot {\rm exp} \left [ - \hspace{0.05cm}\frac{(x - m_1)^2}{2 \sigma^2}\right ]$$

unabhängig vom Mittelwert $m_1$ zur maximalen differentiellen Entropie:

$$h(X) = 1/2 \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.3cm}\Rightarrow\hspace{0.3cm}{\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08\hspace{0.05cm}.$$

Sie finden den Beweis am Ende dieses Kapitels.

Diese Aussage bedeutet gleichzeitig, dass für jede andere WDF als die Gaußverteilung die Kenngröße ${\it \Gamma}_{\rm L} < 2π{\rm e} ≈ 17.08$ sein wird. Beispielsweise ergibt sich der Kennwert

für die Dreieckverteilung zu ${\it \Gamma}_{\rm L} = 6{\rm e} ≈ 16.31$,
für die Laplaceverteilung zu ${\it \Gamma}_{\rm L} = 2{\rm e}^2 ≈ 14.78$, und
für die Gleichverteilung zu $Γ_{\rm L} = 12$ .

Beweis: Maximale differentielle Entropie bei Spitzenwertbegrenzung

Unter der Nebenbedingung der Spitzenwertbegrenzung ⇒ $|X| ≤ A$ gilt für die differentielle Entropie:

$$h(X) = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Von allen möglichen Wahrscheinlichkeitsdichtefunktionen $f_X(x)$, die die Bedingung

$$\int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x = 1$$

erfüllen, ist nun diejenige Funktion $g_X(x)$ gesucht, die zur maximalen differentiellen Entropie $h(X)$ führt.

Zur Herleitung benutzen wir das Verfahren der Lagrange–Multiplikatoren:

Wir definieren die Lagrange–Kenngröße $L$ in der Weise, dass darin sowohl $h(X)$ als auch die Nebenbedingung $|X| ≤ A$ enthalten sind:

$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.5cm}+ \hspace{0.5cm} \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Wir setzen allgemein $f_X(x) = g_X(x) + ε · ε_X(x)$, wobei $ε_X(x)$ eine beliebige Funktion darstellt, mit der Einschränkung, dass die WDF–Fläche gleich $1$ sein muss. Damit erhalten wir:

$$\begin{align*}L = \hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) ] \cdot {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) + \varepsilon \cdot \varepsilon_X(x) } \hspace{0.1cm}{\rm d}x + \lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \big [ g_X(x) + \varepsilon \cdot \varepsilon_X(x) \big ] \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.\end{align*}$$

Die bestmögliche Funktion ergibt sich dann, wenn es für $ε = 0$ eine stationäre Lösung gibt:

$$\left [\frac{{\rm d}L}{{\rm d}\varepsilon} \right ]_{\varepsilon \hspace{0.05cm}= \hspace{0.05cm}0}=\hspace{0.1cm} \hspace{0.05cm} \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \cdot \big [ {\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 \big ]\hspace{0.1cm}{\rm d}x \hspace{0.3cm} + \hspace{0.3cm}\lambda \cdot \int_{-A}^{+A} \hspace{0.05cm} \varepsilon_X(x) \hspace{0.1cm}{\rm d}x \stackrel{!}{=} 0 \hspace{0.05cm}.$$

Diese Bedingungsgleichung ist unabhängig von $ε_X$ nur dann zu erfüllen, wenn gilt:

$${\rm log} \hspace{0.1cm} \frac{1}{ g_X(x) } -1 + \lambda = 0 \hspace{0.4cm} \forall x \in [-A, +A]\hspace{0.3cm} \Rightarrow\hspace{0.3cm} g_X(x) = {\rm const.}\hspace{0.4cm} \forall x \in [-A, +A]\hspace{0.05cm}.$$

$\text{Resümee bei Spitzenwertbegrenzung:}$

Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung $ \vert X \vert ≤ A$ für die Gleichverteilung (englisch: Uniform PDF):

$$h_{\rm max}(X) = {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\rm A} \cdot A) = {\rm log} \hspace{0.1cm} (2A) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm A} = 2 \hspace{0.05cm}.$$

Jede andere Zufallsgröße mit der WDF–Eigenschaft $f_X(\vert x \vert > A) = 0$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch den Parameter ${\it \Gamma}_{\rm A} < 2$.

Beweis: Maximale differentielle Entropie bei Leistungsbegrenzung

Vorneweg zur Begriffserklärung:

Eigentlich wird nicht die Leistung ⇒ das zweite Moment $m_2$ begrenzt, sondern das zweite Zentralmoment ⇒ Varianz $μ_2 = σ^2$.
Gesucht wird also nun die maximale differentielle Entropie unter der Nebenbedingung ${\rm E}\big[|X – m_1|^2 \big] ≤ σ^2$.
Das $≤$–Zeichen dürfen wir hierbei durch das Gleichheitszeichen ersetzen.

Lassen wir nur mittelwertfreie Zufallsgrößen zu, so umgehen wir das Problem. Damit lautet die Lagrange-Multiplikator:

$$L= \hspace{0.1cm} \hspace{0.05cm} \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \cdot {\rm log} \hspace{0.1cm} \frac{1}{ f_X(x) } \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_1 \cdot \int_{-\infty}^{+\infty} \hspace{-0.1cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.1cm}+ \hspace{0.1cm} \lambda_2 \cdot \int_{-\infty}^{+\infty}\hspace{-0.1cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Nach ähnlichem Vorgehen wie beim Beweis für Spitzenwertbegrenzung erhält man das Ergebnis, dass die „bestmögliche” WDF $g_X(x)$ proportinonal zu ${\rm e}^{–λ_2 · x^2}$ sein muss ⇒ Gaußverteilung:

$$g_X(x) ={1}/{\sqrt{2\pi \sigma^2}} \cdot {\rm e}^{ - \hspace{0.05cm}{x^2}/{(2 \sigma^2)} }\hspace{0.05cm}.$$

Wir verwenden hier aber für den expliziten Beweis die Kullback–Leibler–Distanz zwischen einer geeigneten allgemeinen WDF $f_X(x)$ und der Gauß–WDF $g_X(x)$:

$$D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} \frac{f_X(x)}{g_X(x)} \hspace{0.1cm}{\rm d}x = -h(X) - I_2\hspace{0.3cm} \Rightarrow\hspace{0.3cm}I_2 = \int_{-\infty}^{+\infty} \hspace{0.02cm} f_X(x) \cdot {\rm ln} \hspace{0.1cm} {g_X(x)} \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Zur Vereinfachung wurde hier der natürliche Logarithmus ⇒ $\ln$ verwendet. Damit erhalten wir für das zweite Integral:

$$I_2 = - \frac{1}{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{-0.4cm} f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.3cm}- \hspace{0.3cm} \frac{1}{2\sigma^2} \cdot \hspace{-0.1cm}\int_{-\infty}^{+\infty} \hspace{0.02cm} x^2 \cdot f_X(x) \hspace{0.1cm}{\rm d}x \hspace{0.05cm}.$$

Das erste Integral ist definitionsgemäß gleich $1$ und das zweite Integral ergibt $σ^2$:

$$I_2 = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi\sigma^2) - {1}/{2} \cdot [{\rm ln} \hspace{0.1cm} ({\rm e})] = - {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)$$

$$\Rightarrow\hspace{0.3cm} D(f_X \hspace{0.05cm} || \hspace{0.05cm}g_X) = -h(X) - I_2 = -h(X) + {1}/{2} \cdot {\rm ln} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$

Da auch bei wertkontinuierlichen Zufallsgrößen die Kullback–Leibler–Distanz stets $\ge 0$ ist, erhält man nach Verallgemeinerung („ln” ⇒ „log”):

$$h(X) \le {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2)\hspace{0.05cm}.$$

Das Gleichzeichen gilt nur, wenn die Zufallsgröße $X$ gaußverteilt ist.

$\text{Resümee bei Leistungsbegrenzung:}$

Die maximale differentielle Entropie ergibt sich unter der Nebenbedingung ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ unabhängig vom Mittelwert $m_1$ für die Gaußverteilung (englisch: Gaussian PDF):

$$h_{\rm max}(X) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} ({\it \Gamma}_{\hspace{-0.01cm} \rm L} \cdot \sigma^2) = {1}/{2} \cdot {\rm log} \hspace{0.1cm} (2\pi{\rm e} \cdot \sigma^2) \hspace{0.5cm} \Rightarrow\hspace{0.5cm} {\it \Gamma}_{\rm L} = 2\pi{\rm e} \hspace{0.05cm}.$$

Jede andere wertkontinuierliche Zufallsgröße $X$ mit Varianz ${\rm E}\big[ \vert X – m_1 \vert ^2 \big] ≤ σ^2$ führt zu einer kleineren differentiellen Entropie, gekennzeichnet durch die Kenngröße ${\it \Gamma}_{\rm L} < 2πe$.

Aufgaben zum Kapitel

Aufgabe 4.1: WDF, VTF und Wahrscheinlichkeit

Aufgabe 4.1Z: Momentenberechnung

Aufgabe 4.2: Dreieckförmige WDF

Aufgabe 4.2Z: Gemischte Zufallsgrößen

Aufgabe 4.3: WDF–Vergleich bezüglich der differentiellen Entropie

Aufgabe 4.3Z: Exponential– und Laplaceverteilung

Aufgabe 4.4: Herkömmliche Entropie und differenzielle Entropie