Rauscheinfluss bei Winkelmodulation
Signal–zu–Rausch–Leistungsverhältnis bei PM
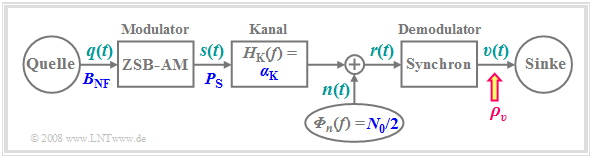
Zur Untersuchung des Rauschverhaltens gehen wir wieder vom so genannten AWGN–Kanal aus und berechnen das Sinken–SNR $ρ_υ$ in Abhängigkeit
- der Frequenz (Bandbreite) $B_{\rm NF}$ des cosinusförmigen Quellensignals,
- der Sendeleistung $P_{\rm S}$,
- des Kanaldämpfungsfaktors $α_{\rm K}$, und
- der (einseitigen) Rauschleistungsdichte $N_0$.
Eine ausführliche Modellbeschreibung findet man im Kapitel 1.2.
Ist die Leistungskenngröße
$$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
Das bedeutet, dass das Sinken–SNR mit wachsendem $η$ quadratisch zunimmt.
Die exakte Berechnung von $ρ_υ$ ist nicht ganz einfach und auch langwierig. Hier soll nur der Rechenweg kurz geschildert werden:
- Man approximiert das weiße Rauschen $n(t)$ mit der Bandbreite $B_{\rm HF}$ durch eine Summe von Sinusstörern im Abstand $f_{\rm St}$ (siehe Skizze im nächsten Abschnitt).
- Man berechnet für jeden einzelnen Sinusstörer das S/N–Verhältnis nach der Demodulation und addiert die einzelnen Beiträge, die nun alle im Tiefpassbereich $|f| < B_{\rm NF}$ liegen.
- Das obige einfache Ergebnis erhält man nach dem Grenzübergang $f_{\rm St} →$ 0. Die Summe geht dann in ein Integral über und dieses kann unter Ausnutzung einiger Näherungen gelöst werden.
Signal–zu–Rausch–Leistungsverhältnis bei FM
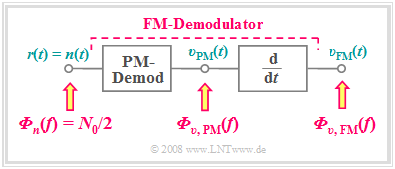
Zur Berechnung nutzt man hier die Tatsache, dass der FM–Demodulator mit einem PM–Demodulator und einem Differenzierer realisiert werden kann. Das nachfolgende Blockschaltbild bezieht sich allein auf die Rauschsignale ⇒ $s(t) =$ 0. Damit ist das Empfangssignal $r(t)$ gleich $n(t)$, wobei für $n(t)$ additives weißes Gaußsches Rauschen mit der Mittenfrequenz $f_{\rm T}$ und der Bandbreite $B_{\rm HF}$ anzusetzen ist.
Bei der Berechnung der Rauschleistungsdichte nach dem FM–Demodulator ist zu berücksichtigen:
- Die Rauschleistungsdichte ${\it Φ}_{\rm υ, PM}(f)$ nach dem PM–Demodulator liegt im Tiefpassbereich, besitzt die (einseitige) Bandbreite $B_{\rm NF}$ und ist ebenfalls „weiß” (siehe linke untere Skizze).
- Die Leistungsdichte am Ausgang eines linearen Systems mit Frequenzgang $H(f)$ lautet allgemein, wenn am Eingang die Rauschleistungsdichte ${\it Φ}_{\rm υ, PM}(f)$ anliegt:
$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} } (f) \cdot |H(f)|^2 \hspace{0.05cm}.$$
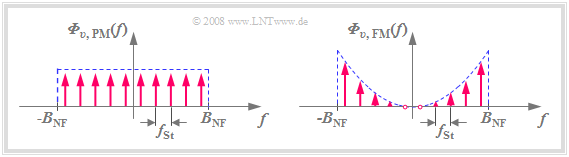
- Der Differenzierer ist ein solches lineares System. Sein Frequenzgang $H(f)$ steigt linear mit $f$ an, und es gilt für die Rauschleistungsdichte am Ausgang des FM-Demodulators (siehe rechte Skizze):
$${ \it \Phi}_{v {\rm , \hspace{0.05cm}FM} } (f) = {\rm const. } \cdot f^2 \cdot { \it \Phi}_{v {\rm , \hspace{0.05cm}PM} }(f) \hspace{0.05cm}.$$
- Berücksichtigt man dieses Ergebnis, so kommt man nach längerer Rechnung zum folgenden Sinken–SNR, falls die Leistungskenngröße $ξ$ hinreichend groß ist:
$$\rho_{v } \approx \frac{3\eta^2}{2} \cdot \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} = 3/2 \cdot{\eta^2} \cdot\xi \hspace{0.05cm}.$$
Die Grafik verdeutlicht, dass ${\it Φ}_{\rm υ, FM}(f)$ im Gegensatz zu ${\it Φ}_{\rm υ, PM}(f)$ nicht weiß ist, sondern zu den Grenzen hin quadratisch ansteigt. Bei der Frequenz $f =$ 0 besitzt ${\it Φ}_{\rm υ, FM}(f)$ dagegen keine Rauschanteile.