Aufgabe 4.3Z: Diracförmige 2D-WDF

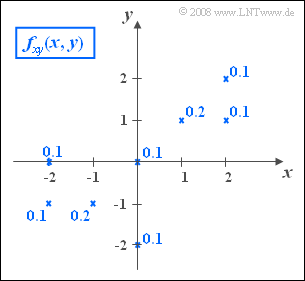
In der Grafik rechts ist die zweidimensionale Wahrscheinlichkeitsdichtefunktion f_xy(x, y) der zwei diskreten Zufallsgrößen x und y dargestellt. Diese 2D–WDF besteht aus acht Diracpunkten, durch Kreuze markiert. Die Zahlenwerte geben die entsprechenden Wahrscheinlichkeiten an.

Es ist zu erkennen, dass sowohl x als auch y alle ganzzahligen Werte zwischen den Grenzen –2 und +2 annehmen können.

Die Varianzen der beiden Zufallsgrößen sind wie folgt gegeben: σ_x² = 2 und σ_y² = 1.4.

Hinweis: Diese Aufgabe bezieht sich auf die Thematik von Kapitel 2.2 und Kapitel 4.1.

Fragebogen

	Die Wahrscheinlichkeiten für –2, –1, 0, +1 und +2 sind gleich.
	Die Zufallsgröße x ist mittelwertfrei (m_x = 0).
	Die Wahrscheinlichkeit Pr(x ≤ 1) ist 0.9.

	Die Wahrscheinlichkeiten für –2, –1, 0, +1 und +2 sind gleich.
	Die Zufallsgröße y ist mittelwertfrei (m_y = 0).
	Die Wahrscheinlichkeit Pr(y ≤ 1) ist 0.9.

$F_\text{xy}(1, 1)$ =

$Pr(x ≤ 1 | y ≤ 1)$ =

$m_\text{xy}$ =

$\theta_\text{y→ x}$ =

Grad

	Die Zufallsgrößen x und y sind statistisch unabhängig.
	Man erkennt bereits aus der vorgegebenen 2D-WDF, dass x und y statistisch voneinander abhängen.
	Aus dem berechneten Korrelationskoeffizienten ρ_xy kann man auf die statistische Abhängigkeit zwischen x und y schließen.

Musterlösung

1. Die Randwahrscheinlichkeitsdichtefunktion f_x(x) erhält man aus der 2D–WDF f_xy(x, y) durch Integration über y. Für alle möglichen Werte x ∈ {–2, –1, 0, 1, 2} sind die Wahrscheinlichkeiten gleich 0.2, und es gilt Pr(x ≤ 1) = 0.8. Der Mittelwert ist m_x = 0. Richtig sind somit die beiden ersten Antworten.

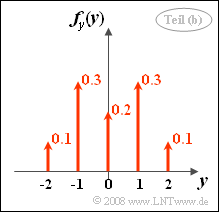
2. Durch Integration über x erhält man die rechts skizzierte WDF. Aufgrund der Symmetrie ergibt sich der Mittelwert m_y = 0. Die gesuchte Wahrscheinlichkeit Pr(y ≤ 1) ist 0.9. Richtig sind also die Lösungsvorschläge 2 und 3.

3. Definitionsgemäß gilt:

$$F_{xy}(r_x, r_y) = \rm Pr((\it x \le r_x)\cap(\it y\le r_y)).$$

Für r_x = r_y = 1 folgt daraus:

$$F_{xy}(\rm 1, \rm 1) = \rm Pr((\it x \le \rm 1)\cap(\it y\le \rm 1)).$$

Wie aus der 2D–WDF auf der Angabenseite zu ersehen, ist diese Wahrscheinlichkeit gleich 0.8.

4. Hierfür kann mit dem Satz von Bayes auch geschrieben werden:

$$ \rm Pr(\it x \le \rm 1)\hspace{0.05cm} | \hspace{0.05cm} \it y \le \rm 1) = \frac{ \rm Pr((\it x \le \rm 1)\cap(\it y\le \rm 1))}{ \rm Pr(\it y\le \rm 1)} = \it \frac{F_{xy}(\rm 1, \rm 1)}{F_{y}(\rm 1)}.$$

Mit den Ergebnissen aus (2) und (3) folgt daraus Pr(x ≤ 1 | y ≤ 1) = 0.8/0.9 = 8/9 = 0.889.

5. Entsprechend der Definition gilt für das gemeinsame Moment:

$$m_{xy} = \rm E[\it x\cdot y] = \sum\limits_{i} \rm Pr(\it x_i \cap y_i)\cdot \it x_i\cdot y_i. $$

Es verbleiben fünf Diracfunktionen mit x_i · y_i ≠ 0:

$$m_{xy} = \rm 0.1\cdot (-2) (-1) + 0.2\cdot(-1) (-1)+ 0.2\cdot 1\cdot 1 + 0.1\cdot 2\cdot 1+ 0.1\cdot 2\cdot 2\hspace{0.15cm}\underline{=\rm 1.2}.$$

6. Für den Korrelationskoeffizienten gilt:

$$\rho_{xy} = \frac{\mu_{xy}}{\sigma_x\cdot \sigma_y} = \frac{1.2}{\sqrt{2}\cdot\sqrt{1.4}}=0.717.$$

Hier ist berücksichtigt, dass wegen m_x = m_y = 0 die Kovarianz μ_xy gleich dem Moment m_xy ist.

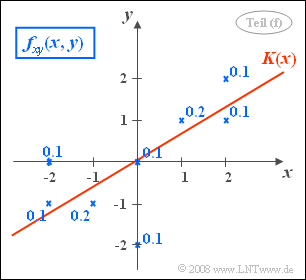
Die Gleichung der Korrelationsgeraden lautet:

$$y=\frac{\sigma_y}{\sigma_x}\cdot \rho_{xy}\cdot x = \frac{\mu_{xy}}{\sigma_x^{\rm 2}}\cdot x = \rm 0.6\cdot \it x.$$

Im Bild ist die Gerade y = K(x) eingezeichnet. Der Winkel zwischen Korrelationsgerade und x-Achse beträgt θ_y→x = arctan(0.6) ≈ 31°.

7. Bei statistischer Unabhängigkeit müsste f_xy(x, y) = f_x(x) · f_y(y) gelten, was hier nicht erfüllt ist. Aus der Korreliertheit (folgt aus ρ_xy = 0.6) kann direkt auf die statistische Abhängigkeit geschlossen werden, denn Korrelation bedeutet eine Sonderform (nämlich linear) der statistischen Abhängigkeit. Richtig sind die Lösungsvorschläge 2 und 3.