Grundlegendes zu den Produktcodes

Grundstruktur eines Produktcodes

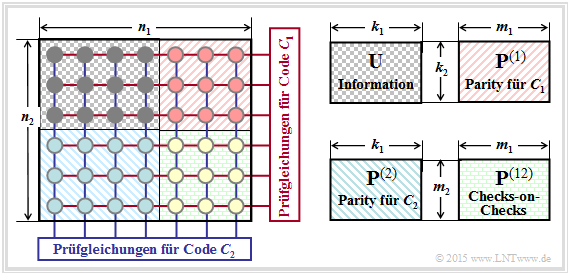
Die Grafik zeigt den prinzipiellen Aufbau von Produktcodes, die bereits 1954 von Peter Elias eingeführt wurden. Der nachfolgend dargestellte zweidimensionale Produktcode C = C₁ × C₂ basiert auf den beiden linearen und binären Blockcodes mit den Parametern (n₁, k₁) bzw. (n₂, k₂).

Die Codewortlänge ist n = n₁ · n₂. Diese n Codebits lassen sich wie folgt gruppieren:

Die k = k₁ · k₂ Informationsbits sind in der k₂×k₁–Matrix U angeordnet. Die Coderate ist gleich dem Produkt der Coderaten der beiden Basiscodes: R = k/n = (k₁/n₁) · (k₂/n₂) = R₁ · R₂.

Die rechte obere Matrix P⁽¹⁾ mit der Dimension k₂×m₁ beinhaltet die Prüfbits (englisch: Parity) hinsichtlich des Codes C₁. In jeder der k₂ Zeilen werden zu den k₁ Informationsbits m₁ = n₁ – k₁ Prüfbits hinzugefügt, wie in Kapitel 1.3 am Beispiel der Hamming–Codes beschrieben wurde.

Die linke untere Matrix P⁽²⁾ der Dimension m₂×k₁ beinhaltet die Prüfbits hinsichtlich des zweiten Komponentencodes C₂. Hier erfolgt die Codierung (und auch die Decodierung) zeilenweise: In jeder der k₁ Spalten werden die k₂ Informationsbits noch um m₂ = n₂ – k₂ Prüfbits ergänzt.

Die m₂×m₁–Matrix P⁽¹²⁾ rechts unten bezeichnet man als Checks–on–Checks. Hier werden die vorher erzeugten Parity–Matrizen P⁽¹⁾ und P⁽²⁾ entsprechend den Prüfgleichungen verknüpft.

Alle Produktcodes entsprechend obiger Grafik weisen folgende Eigenschaften auf:

Bei linearen Komponentencodes C₁ und C₂ ist auch der Produktcode C = C₁ × C₂ linear.

Jede Zeile von C gibt ein Codewort von C₁ wieder und jede Spalte ein Codewort von C₂.

Die Summe zweier Zeilen ergibt aufgrund der Linearität wieder ein Codewort von C₁.

Ebenso ergibt die Summe zweier Spalten ein gültiges Codewort von C₂.

Jeder Produktcodes beinhaltet auch das Nullwort 0 (ein Vektor mit n Nullen).

Die minimale Distanz von C ist d_min = d₁ · d₂, wobei d_i die minimale Distanz von C_i angibt.

Iterative Syndromdecodierung von Produktcodes (1)

Wir betrachten nun den Fall, dass ein Produktcode mit Matrix X über einen Binärkanal übertragen wird. Die Empfangsmatrix sei Y = X + E, wobei E die Fehlermatrix bezeichnet. Alle Elemente der Matrizen X, E und Y seien binär, also 0 oder 1.

Für die Decodierung der beiden Komponentencodes bietet sich die Syndromdecodierung entsprechend dem Kapitel 1.5 an. Im zweidimensionalen Fall bedeutet dies:

Man decodiert zunächst die n₂ Zeilen der Empfangsmatrix Y, basierend auf der Prüfmatrix H₁ des Komponentencodes C₁. Man verwendet hierzu die Syndromdecodierung.

Dazu bildet man jeweils das sogenannte Syndrom s = y · H₁^T, wobei der Vektor y der Länge n₁ die aktuelle Zeile von Y angibt und „T” für „transponiert” steht.

Entsprechend dem berechneten s_μ (mit 0 ≤ μ < 2^n₁–k₁) findet man dann in einer vorbereiteten Syndromtabelle das wahrscheinliche Fehlermuster e = e_μ.

Bei nur wenigen Fehlern innerhalb der Zeile stimmt dann y + e mit dem gesendeten Zeilenvektor x überein. Sind zu viele Fehler aufgetreten, so kommt es allerdings zu Fehlkorrekturen.

Anschließend syndromdecodiert man die n₁ Spalten der (korrigierten) Empfangsmatrix Y', diesmal basierend auf der (transponierten) Prüfmatrix H₂^T des Komponentencodes C₂.

Hierzu bildet man das Syndrom s = y' · H₂^T, wobei der Vektor y' der Länge n₂ die betrachtete Spalte von Y' bezeichnet.

Aus einer zweiten Syndromtabelle (gültig für den Code C₂) findet man für das berechnete s_μ (mit 0 ≤ μ < 2^n₂–k₂) das wahrscheinliche Fehlermuster e = e_μ der bearbeiteten Spalte.

Nach Korrektur aller Spalten liegt die Marix Y vor. Nun kann man wieder eine Zeilen– und anschließend eine Spaltendecodierung vornehmen ⇒ zweite Iteration, und so weiter, und so fort.

Auf der nächsten Seite wird dieser Decodieralgorithmus an einem Beispiel verdeutlicht. Dazu betrachten wir wieder den (42, 12) Produktcode, basierend auf

dem Hammingcode (7, 4, 3) ⇒ Code C₁,

dem verkürzten Hammingcode (6, 3, 3) ⇒ Code C₂.

Die Prüfmatrizen dieser beiden systematischen Komponentencodes lauten in transponierter Form:

\[{ \boldsymbol{\rm H}}_1^{\rm T} = \begin{pmatrix} 1 &0 &1 \\ 1 &1 &0 \\ 0 &1 &1 \\ 1 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix} \hspace{0.05cm}, \hspace{0.5cm} { \boldsymbol{\rm H}}_2^{\rm T} = \begin{pmatrix} 1 &1 &0 \\ 1 &0 &1 \\ 0 &1 &1 \\ 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{pmatrix}\hspace{0.05cm}.\]

Iterative Syndromdecodierung von Produktcodes (2)

Die linke Grafik zeigt die Empfangsmatrix Y, Aus Darstellungsgründen wurde die Codermatrix X zu einer 6 × 7–Nullmatrix gewählt, so dass die neun Einsen in Y gleichzeitig Übertragungsfehler darstellen.

Hinweis: Für die folgenden Berechnungen ist der Link zu den transponierten Prüfmatrizen nützlich.

Die zeilenweise Syndromdecodierung geschieht über das Syndrom s = y · H₁^T. Im Einzelnen:

Zeile 1 ⇒ Einzelfehlerkorrektur ist erfolgreich (ebenso in den Zeilen 3, 4 und 6):

\[\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3\]

\[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]

Zeile 2 ⇒ Fehlkorrektur bezüglich Bit 5:

\[\underline{s} = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4\]

\[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 1, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}1 \right ) \hspace{0.05cm}.\]

Zeile 5 ⇒ Fehlkorrektur bezüglich Bit 3:

\[\underline{s} = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 0, \hspace{0.03cm} 1, \hspace{0.03cm}1 \right ) = \underline{s}_3\]

\[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_3 = \left ( 0, \hspace{0.02cm} 0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]

Die spaltenweisen Syndromdecodierung entfernt alle Einzelfehler in den Spalten 1, 2, 3, 4, 6 und 7.

Spalte 5 ⇒ Fehlkorrektur bezüglich Bit 4:

\[\underline{s} = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{-0.03cm}\cdot \hspace{-0.03cm}{ \boldsymbol{\rm H}}_1^{\rm T} \hspace{-0.05cm}= \left ( 1, \hspace{0.03cm} 0, \hspace{0.03cm}0 \right ) = \underline{s}_4\]

\[\Rightarrow \hspace{0.3cm} \underline{y} + \underline{e}_4 = \left ( 0, \hspace{0.02cm} 1, \hspace{0.02cm}0, \hspace{0.02cm}1, \hspace{0.02cm}1, \hspace{0.02cm}0 \right ) \hspace{0.05cm}.\]

Die verbliebenen drei Fehler werden durch zeilenweise Decodierung der zweiten Iterationsschleife korrigiert.

Ob alle Fehler eines Blockes korrigierbar sind, hängt vom Fehlermuster ab. Hier verweisen wir auf Aufgabe A4.7.