Allgemeine Beschreibung

1. Informationstheorie
2. Quellencodierung – Datenkomprimierung
3. Allgemeine Beschreibung

• Vorherige Seite
• Nächste Seite

• Vorherige Seite
• Nächste Seite

Quellencodierung – Kanalcodierung – Leitungscodierung

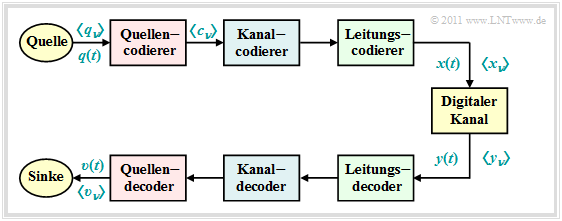
Wir betrachten für die Beschreibungen im Kapitel 2 das folgende digitale Übertragungsmodell:

Zu diesem Modell ist zu bemerken:

• Das Quellensignal $q(t)$ kann ebenso wie das Sinkensignal υ(t) sowohl analog als auch digital sein. Alle anderen Signale in diesem Blockschaltbild – auch die hier nicht explizit benannten – sind Digitalsignale.
• Insbesondere sind auch die Signale $x(t)$ und $y(t)$ am Eingang und Ausgang des Digitalen Kanals digital und können deshalb auch durch die Symbolfolgen $〈x_ν〉$ und $〈y_ν〉$ vollständig beschrieben werden.
• Der „Digitale Kanal” beinhaltet neben dem Übertragungsmedium und den Störungen (Rauschen) auch Komponenten des Senders (Modulator, Sendeimpulsformer, usw.) und des Empfängers (Demodulator, Empfangsfilter bzw. Detektor, Entscheider). Zur Modellierung des Digitalen Kanals sei auf das Kapitel 5 im Buch Digitalsignalübertragung verwiesen.

Wie aus dem obigen Blockschaltbild zu erkennen ist, unterscheidet man je nach Zielrichtung zwischen drei verschiedenen Arten von Codierung, jeweils realisiert durch den sendeseitigen Codierer (Coder) und den zugehörigen Decoder beim Empfänger:

• Die Aufgabe der Quellencodierung ist die Redundanzreduktion zur Datenkomprimierung, wie sie beispielsweise in der Bildcodierung Anwendung findet. Durch Ausnutzung statistischer Bindungen zwischen den einzelnen Punkten eines Bildes bzw. zwischen den Helligkeitswerten eines Punktes zu verschiedenen Zeiten (bei Bewegtbildsequenzen) können Verfahren entwickelt werden, die bei nahezu gleicher Bildqualität zu einer merklichen Verminderung der Datenmenge (gemessen in Bit oder Byte) führen. Ein einfaches Beispiel hierfür ist die differentielle Pulscodemodulation (DPCM).
• Bei der Kanalcodierung erzielt man demgegenüber dadurch eine merkliche Verbesserung des Übertragungsverhaltens, dass eine beim Sender gezielt hinzugefügte Redundanz empfangsseitig zur Erkennung und Korrektur von Übertragungsfehlern genutzt wird. Solche Codes, deren wichtigste Vertreter Blockcodes, Faltungscodes und Turbocodes sind, haben besonders bei stark gestörten Kanälen eine große Bedeutung. Je größer die relative Redundanz des codierten Signals ist, desto besser sind die Korrektureigenschaften des Codes, allerdings bei verringerter Nutzdatenrate.
• Eine Leitungscodierung – häufig auch als Übertragungscodierung bezeichnet – verwendet man, um das Sendesignal durch eine Umcodierung der Quellensymbole an die spektralen Eigenschaften von Kanal und Empfangseinrichtungen anzupassen. Beispielsweise muss bei einem Übertragungskanal, über den kein Gleichsignal übertragen werden kann – für den also $H_K(f$ = 0) = 0 gilt – durch Übertragungscodierung sichergestellt werden, dass die Codesymbolfolge keine langen Folgen gleicher Polarität beinhaltet.

Im Mittelpunkt des vorliegenden Kapitels steht die verlustfreie Quellencodierung, die ausgehend von der Quellensymbolfolge $〈q_ν〉$ eine datenkomprimierte Codesymbolfolge $〈c_ν〉$ generiert, basierend auf den Ergebnissen der Informationstheorie. Der Kanalcodierung ist in unserem Tutorial ein eigenes Buch mit folgendem Inhalt gewidmet. Die Leitungscodierung wird in Kapitel 2 des Buches Digitalsignalübertragung eingehend behandelt. Anmerkung: Wir verwenden hier einheitlich „ν” als Laufvariable einer Symbolfolge. Eigentlich müssten für $〈q_ν〉$, $〈c_ν〉$ und $〈x_ν〉$ unterschiedliche Indizes verwendet werden, wenn die Raten nicht übereinstimmen.

Verlustbehaftete Quellencodierung

Ein erstes Beispiel für Quellencodierung ist die 1938 erfundene Pulscodemodulation (PCM), die aus einem analogen Quellensignal q(t) durch

• Abtastung
• Quantisierung
• PCM–Codierung

die Codesymbolfolge $〈c_ν〉$ extrahiert. Wegen der erforderlichen Bandbegrenzung und der Quantisierung ist diese Umformung jedoch stets verlustbehaftet. Das bedeutet, dass die codierte Folge $〈c_ν〉$ nicht die gesamte Information des Quellensignals $q(t)$ beinhaltet, und dass sich das Sinkensignal $v(t)$ grundsätzlich von $q(t)$ unterscheidet. Meist ist die Abweichung allerdings nicht sehr groß.

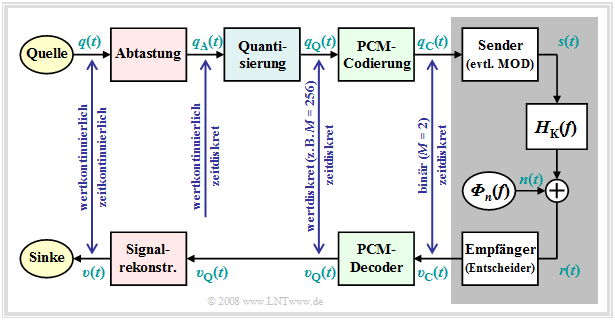
Die Grafik verdeutlicht das PCM–Prinzip. Die zugehörige Bildbeschreibung findet man auf den ersten Seiten von Kapitel 4.1 im Buch Modulationsverfahren.

Wird ein Sprachsignal spektral auf die Bandbreite $B$ = 4 kHz ⇒ Abtastrate $f_A$ = 8 kHz begrenzt, so ergibt sich bei Quantisierung mit 13 Bit ⇒ Quantisierungsstufenzahl M = $2^13$ = 8192 ein binärer Datenstrom der Datenrate $R$ = 104 kbit/s. Die Daten entstammen der GSM–Spezifikation. Der Quantisierungsrauschabstand beträgt dann 20 · lg $M$ ≈ 78 dB. Bei Quantisierung mit 16 Bit würde sich dieser auf etwa 96 dB erhöhen, aber gleichzeizig steigt dadurch die erforderliche Datenrate auf 128 kbit/s. Die Auswirkungen der Bandbegrenzung auf ein Sprachsignal bzw. Musiksignal können Sie sich mit dem folgenden Interaktionsmodul verdeutlichen: Einfluss einer Bandbegrenzung bei Sprache und Musik

Der Standard ISDN (Integrated Services Digital Network) für Telefonie über Zweidrahtleitung basiert auf dem PCM–Prinzip, wobei jedem Teilnehmer zwei B–Kanäle (Bearer Channels) mit je 64 kbit/s ⇒ $M$ = $2^8$ = 256 und ein D–Kanal (Data Channel) mit 16 kbit/s zur Verfügung gestellt wird. Die Nettodatenrate beträgt somit 144 kbit/s. Unter Berücksichtigung der Kanalcodierung und der Steuerbits (aus organisatorischen Gründen erforderlich) kommt man auf die ISDN–Bruttodatenrate von 192 kbit/s.

Im Mobilfunk können sehr große Datenraten oft (noch) nicht bewältigt werden. Hier wurden in den 1990er–Jahren Sprachcodierverfahren entwickelt, die zu einer Datenkomprimierung um den Faktor 8 und mehr führen. Zu erwähnen sind aus heutiger Sicht:

• der Enhanced Full–Rate Codec (EFR), der pro Sprachrahmen von 20 ms genau 244 Bit extrahiert (Datenrate: 12.2 kbit/s); erreicht wird diese Datenkomprimierung um mehr als den Faktor 8 durch die Aneinanderreihung mehrerer Verfahren: Linear Predictive Coding (LPC, Kurzzeitprädiktion), Long Term Prediction (LTP, Langzeitprädiktion) und Regular Pulse Excitation (RPE);
• der Adaptive Multi–Rate Codec (AMR), der auf ACELP (Algebraic Code Excited Linear Prediction) basiert und mehrere Modi zwischen 12.2 kbit/s (EFR) und 4.75 kbit/s bereit stellt, so dass bei schlechterer Kanalqualität eine verbesserte Kanalcodierung eingesetzt werden kann;
• der Wideband–AMR (WB–AMR) mit neun Modi zwischen 6.6 kbit/s und 23.85 kbit/s. Dieser wird bei UMTS eingesetzt und ist für breitbandigere Signale zwischen 200 Hz und 7 kHz geeignet. Die Abtastung erfolgt mit 16 kHz, die Quantisierung mit 4 Bit.

Das Audio–Interaktionsmodul Qualität verschiedener Sprach–Codecs vergleicht diese Codecs. Zur Digitalisierung analoger Quellensignale wie Sprache, Musik oder Bilder können nur verlustbehaftete Quellencodierverfahren verwendet werden. Bereits die Speicherung eines Fotos im BMP–Format ist aufgrund von Abtastung, Quantisierung und der endlichen Farbtiefe stets mit einem Informationsverlust verbunden. Daneben gibt es aber auch eine Vielzahl von Kompressionsverfahren für Bilder, die zu deutlich kleineren Bilddateien als „BMP” führen, zum Beispiel:

• GIF (Graphics Interchange Format), 1987 von Steve Wilhite entwickelt.
• JPEG – ein Format, das 1992 von der Joint Photographie Experts Group vorgestellt wurde und heute der Standard für Digitalkameras ist. Endung: „jpeg” bzw. „jpg”.
• TIFF (Tagged Image File Format), um 1990 von Aldus Corp. (jetzt Adobe) und Microsoft entwickelt, ist noch heute der Quasi–Standard für druckreife Bilder höchster Qualität.
• PNG (Portable Network Graphics), 1995 von Thomas Boutell und Tom Lane entworfen als Ersatz für das durch Patentforderungen belastete GIF–Format; weniger komplex als TIFF.

Diese Kompressionsverfahren nutzen teilweise Vektorquantisierung zur Redundanzminderung korrelierter Bildpunkte, gleichzeitig die verlustlosen Kompressionsalgorithmen nach Huffman und Lempel/Ziv, eventuell auch Transformationscodierungen basierend auf DFT (Diskrete Fouriertransformation) und DCT (Diskrete Cosinustransformation), danach Quantisierung und Übertragung im transformierten Bereich.

Wir vergleichen nun die Auswirkungen von

• JPEG (mit Komprimierungsfaktor 8) und
• PNG (mit Komprimierungsfaktor 24)

auf die subjektive Qualität von Fotos und Grafiken.

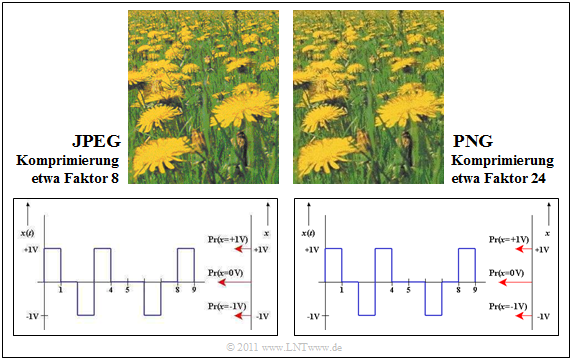
Im oberen Teil der folgenden Grafik sehen Sie zwei Komprimierungen eines Fotos. Das Format JPEG (linke Darstellung) ermöglicht gegenüber der pixelweisen Abspeicherung einen Komprimierungsfaktor von 8 bis 15 bei (nahezu) verlustfreier Komprimierung. Selbst mit dem Faktor 35 kann das Ergebnis noch als „gut” bezeichnet werden.

Das rechts dargestellte Bild wurde mit PNG komprimiert. Die Qualität ist vergleichbar mit dem linken JPEG–Bild, obwohl die Komprimierung um etwa den Faktor 3 stärker ist. Dagegen erzielt PNG ein schlechteres Komprimierungsergebnis als JPEG, wenn das Foto sehr viele Farbstufungen enthält. Bei den meisten Digitalkameras für den Consumer–Bereich ist JPEG das voreingestellte Speicherformat.

Auch bei Strichzeichnungen mit Beschriftungen ist PNG besser geeignet als JPEG (untere Bilder). Die Qualität der JPEG–Komprimierung (links) ist deutlich schlechter als das PNG–Resultat, obwohl die resultierende Dateigröße etwa dreimal so groß ist. Insbesondere Schriften wirken „verwaschen”.

Anmerkung: Aufgrund technischer Einschränkungen bei LNTwww mussten alle Grafiken als PNG gespeichert werden. In obiger Grafik bedeutet also „JPEG” die PNG–Konvertierung einer zuvor mit JPEG komprimierten Datei. Der damit zusammenhängende Verlust ist jedoch vernachlässigbar.

MPEG–2 Audio Layer III – kurz MP3

Das heute (2015) am weitesten verbreitete Kompressionsverfahren für Audiodateien ist MP3. Entwickelt wurde dieses Format ab 1982 am Fraunhofer–Institut für Integrierte Schaltungen (IIS) in Erlangen unter der Federführung von Prof. Hans–Georg Musmann in Zusammenarbeit mit der Friedrich–Alexander–Universität Erlangen–Nürnberg und den AT&T Bell Labs. Auch andere Institutionen machen diesbezügliche Patentansprüche geltend, so dass seit 1998 zu verschiedene Klagen gab, die nach Kenntnis der Autoren noch nicht endgültig abgeschlossen sind. Im Folgenden werden einige Maßnahmen genannt, die bei MP3 genutzt werden, um die Datenmenge gegenüber der Raw–Version im WAV–Format zu reduzieren. Die Zusammenstellung ist nicht vollständig. Eine umfassende Darstellung findet man zum Beispiel im Wikipedia Artikel hierzu.

• Das Audio–Kompressionsverfahren MP3 nutzt unter anderem auch psychoakustische Effekte der Wahrnehmung aus. So kann der Mensch zwei Töne erst ab einem gewissen Mindestunterschied der Tonhöhe voneinander unterscheiden. Man spricht von so genannten „Maskierungseffekten”.
• Die Maskierungseffekte ausnutzend werden bei MP3 Signalanteile, die für den Höreindruck minderwichtig sind, mit weniger Bit (verringerte Genauigkeit) gespeichert. Ein dominanter Ton bei 4 kHz kann beispielsweise dazu führen, dass benachbarte Frequenzen bis zu 11 kHz für das momentane Hörempfinden nur eine untergeordnete Bedeutung besitzen.
• Die größte Ersparnis der MP3–Codierung liegt aber daran, dass die Töne mit gerade so vielen Bits abgespeichert werden, dass das dadurch entstehende Quantisierungsrauschen noch maskiert wird und nicht hörbar ist.
• Weitere MP3–Kompressionsmechanismen sind die Ausnutzung der Korrelationen zwischen den beiden Kanälen eines Stereosignals durch Differenzbildung sowie die Huffman–Codierung des resultierenden Datenstroms. Beide Maßnahmen sind verlustlos.

Nachteil der MP3–Codierung ist, dass bei starker Kompression auch „wichtige” Frequenzanteile von der Kompression erfasst werden und es dadurch zu hörbaren Fehlern kommt. Ferner ist es störend, dass aufgrund der blockweisen Anwendung des MP3–Verfahrens am Ende einer Datei Lücken entstehen können. Abhilfe schafft die Verwendung des so genannten LAME–Coders – ein Open–Source–Project – und eines entsprechenden Abspielprogramms.

Voraussetzungen für Kapitel 2

Im Folgenden betrachten wir ausschließlich verlustlose Quellencodierverfahren und gehen dabei von folgenden Annahmen aus:

• Die digitale Quelle besitze den Symbolumfang $M$. Für die einzelnen Quellensymbole der Folge $〈q_ν〉$ gelte mit dem Symbolvorrat { $q_μ$ }:

$$q_{\nu} \in \{ q_{\mu} \}\hspace{0.05cm}, \hspace{0.2cm}\mu = 1, ... \hspace{0.05cm}, M \hspace{0.05cm}. $$

• Die einzelnen Folgenelemente $q_ν$ können statistisch unabhängig sein oder auch statistische Bindungen aufweisen. Zunächst betrachten wir Nachrichtenquellen ohne Gedächtnis, die durch die Symbolwahrscheinlichkeiten vollständig charakterisiert sind; zum Beispiel:

$M$ = 4: $q_μ$ ∈ {A, B, C, D}, mit den Wahrscheinlichkeiten $p_A$, $p_B$, $p_C$, $p_D$,

$M$ = 8: $q_μ$ ∈ {A, B, C, D, E, F, G, H}, Wahrscheinlichkeiten $p_A$, ... , $p_H$.

• Der Quellencodierer ersetzt das Quellensymbol qμ durch das Codewort $C(q_μ)$, bestehend aus $L_μ$ Codesymbolen eines neuen Alphabets {0, 1, ... , $D$ – 1} mit dem Symbolumfang $D$. Damit ergibt sich für die mittlere Codewortlänge:

$$L_{\rm M} = \sum_{\mu=1}^{M} \hspace{0.1cm} p_{\mu} \cdot L_{\mu} \hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.2cm}p_{\mu} = {\rm Pr}(q_{\mu}) \hspace{0.05cm}. $$

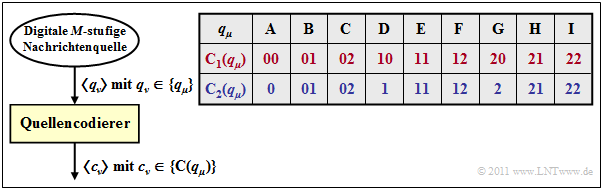
Wir betrachten zwei verschiedene Quellencodierungen, jeweils mit den Parametern $M$ = 9 und $D$ = 3. Bei der ersten Codierung $C_1(q_μ)$ entsprechend Zeile 2 (rote Darstellung) wird jedes Quellensymbol qμ durch zwei Ternärsymbole (0, 1 oder 2) ersetzt. Beispielsweise gilt die Zuordnung:

A C F B I G ⇒ 00 02 12 01 22 20

Bei dieser Codierung haben alle Codeworte $C_1(q_μ)$ mit 1 ≤ $μ$ ≤ 9 die gleiche Länge $L_μ$ = 2. Damit ist auch die mittlere Codewortlänge $L_M$ = 2.

Dagegen gilt beim zweiten, dem blauen Quellencodierer $L_μ$ ∈ {1, 2} und dementsprechend wird die mittlere Codewortlänge kleiner sein als zwei Codesymbole pro Quellensymbol. Hier gilt die Zuordnung:

A C F B I G ⇒ 0 02 12 01 22 2.

Es ist offensichtlich, dass diese zweite Codesymbolfolge nicht eindeutig decodiert werden kann.

Kraftsche Ungleichung – Präfixfreie Codes

Codes zur Komprimierung einer gedächtnislosen wertdiskreten Quelle zeichnen sich dadurch aus, dass die einzelnen Symbole durch verschieden lange Codesymbolfolgen dargestellt werden:

$$L_{\mu} \ne {\rm const.} \hspace{0.4cm}(\mu = 1, ... \hspace{0.05cm}, M ) \hspace{0.05cm}.$$

Nur dann ist es möglich,

• dass die mittlere Codewortlänge minimal wird,
• falls die Quellensymbole nicht gleichwahrscheinlich sind.

Um eine eindeutige Decodierung zu ermöglichen, muss der Code zudem „präfixfrei” sein.

Die Eigenschaft präfixfrei sagt aus, dass kein Codewort der Präfix (der Beginn) eines längeren Codewortes sein darf. Ein solcher präfixfreier Code ist sofort decodierbar.

Der zweite (blaue) Code im Beispiel ist nicht präfixfrei. Beispielsweise könnte die Codesymbolfolge „01” vom Decoder als AD interpretiert werden, aber ebenso als B. Dagegen ist der rote Code präfixfrei, wobei hier die Präfixfreiheit wegen $L_μ$ = const. nicht unbedingt erforderlich wäre. Die notwendige Bedingung für die Existenz eines präfixfreien Codes wurde von Leon Kraft in seiner Master Thesis 1949 am Massachusetts Institute of Technology (MIT) angegeben. :

$$\sum_{\mu=1}^{M} \hspace{0.2cm} D^{-L_{\mu}} \le 1 \hspace{0.05cm}.$$

Überprüft man den zweiten (blauen) Code des betrachteten Beispiels mit $M$ = 9 und $D$ = 3, so erhält man:

$$3 \cdot 3^{-1} + 6 \cdot 3^{-2} = 1.667 > 1 \hspace{0.05cm}.$$

Daraus ist ersichtlich, dass dieser Code nicht präfixfrei sein kann.

Betrachten wir den binären Code

$$\boldsymbol[[:Vorlage:\rm A]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 0 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm B]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 00 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm C]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 11 \hspace{0.05cm}, $$

so ist dieser offensichtlich nicht präfixfrei. Die Gleichung

$$1 \cdot 2^{-1} + 2 \cdot 2^{-2} = 1 $$

sagt also keinesfalls aus, dass dieser Code tatsächlich präfixfrei ist, sondern es bedeutet lediglich, dass es einen präfixfreien Code mit gleicher Längenverteilung gibt, zum Beispiel

$$\boldsymbol[[:Vorlage:\rm A]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 0 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm B]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 10 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm C]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 11 \hspace{0.05cm}.$$

Quellencodierungstheorem

Wir betrachten eine redundante Nachrichtenquelle mit dem Symbolvorrat { $q_μ$ }, wobei die Laufvariable $μ$ alle Werte zwischen 1 und dem Symbolumfang $M$ annimmt. Die Quellenentropie $H$ sei kleiner als der Nachrichtengehalt $H_0$. Die Redundanz $H_0$ – $H$ geht entweder zurück

• auf nicht gleichwahrscheinliche Symbole ⇒ $p_μ$ ≠ 1/ $M$, und/oder
• auf statistische Bindungen innerhalb der Folge $〈qμ〉$.

Ein Quellencodierer ersetzt das Quellensymbol $q_μ$ durch das binäre Codewort $C(q_μ)$, bestehend aus $L_μ$ Binärsymbolen (Nullen oder Einsen). Damit ergibt sich die mittlere Codewortlänge zu

$$L_{\rm M} = \sum_{\mu=1}^{M} \hspace{0.2cm} p_{\mu} \cdot L_{\mu} \hspace{0.05cm}, \hspace{0.2cm}{\rm mit} \hspace{0.2cm}p_{\mu} = {\rm Pr}(q_{\mu}) \hspace{0.05cm}. $$

Für die hier beschriebene Quellencodierungsaufgabe kann folgende Grenze angegeben werden:

Shannons Quellencodierungstheorem: Für die vollständige Rekonstruktion der gesendeten Zeichenfolge aus der Binärfolge ist es hinreichend, aber auch notwendig, dass man zur sendeseitigen Codierung im Mittel $H$ Binärsymbole pro Quellensymbol verwendet. Das heißt, dass die mittlere Codewortlänge auf keinen Fall kleiner sein kann als die Entropie $H$ der Quellensymbolfolge:

$$L_{\rm M} \ge H \hspace{0.05cm}. $$

Berücksichtigt der Quellencodierer nur die unterschiedlichen Auftrittswahrscheinlichkeiten, nicht aber die inneren statistischen Bindungen, dann gilt $L_M ≥ H_1$ ⇒ erste Entropienäherung.

Bei einer Quaternärquelle mit den Symbolwahrscheinlichkeiten

$$p_{\rm A} = 2^{-1}\hspace{0.05cm}, \hspace{0.2cm}p_{\rm B} = 2^{-2}\hspace{0.05cm}, \hspace{0.2cm}p_{\rm C} = p_{\rm D} = 2^{-3} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H = H_1 = 1.75\,\, {\rm bit/Quellensymbol} $$

ergibt sich in obiger Gleichung das Gleichheitszeichen ⇒ $L_M = H$, wenn man zum Beispiel folgende Zuordnung wählt:

$$\boldsymbol[[:Vorlage:\rm A]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 0 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm B]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 10 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm C]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 110 \hspace{0.05cm}, \hspace{0.2cm}\boldsymbol[[:Vorlage:\rm D]] \hspace{0.15cm} \Rightarrow \hspace{0.15cm} 111 \hspace{0.05cm}. $$

Dagegen ergibt sich mit der gleichen Zuordnung und

$$p_{\rm A} = 0.4\hspace{0.05cm}, \hspace{0.2cm}p_{\rm B} = 0.3\hspace{0.05cm}, \hspace{0.2cm}p_{\rm C} = 0.2 \hspace{0.05cm}, \hspace{0.2cm}p_{\rm D} = 0.1\hspace{0.05cm} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} H = 1.845\,\, {\rm bit/Quellensymbol}$$

die mittlere Codewortlänge

$$L_{\rm M} = 0.4 \cdot 1 + 0.3 \cdot 2 + 0.2 \cdot 3 + 0.1 \cdot 3 = 1.9\,\, {\rm bit/Quellensymbol}\hspace{0.05cm}. $$

Wegen der ungünstigen Symbolwahrscheinlichkeiten (keine Zweierpotenzen) ist hier $L_M > H$.

Es folgt ein zweites Beispiel, wobei die Quellensymbolfolge einen natürlichen Text beschreibt.

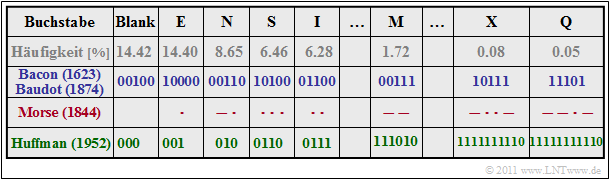
Beispiel 2: Betrachten wir noch frühere Versuche der Quellencodierung für die Übertragung von Texten, wobei wir von den in der Tabelle angegebenen Buchstabenhäufigkeiten ausgehen. In der Literatur findet man eine Vielzahl unterschiedlicher Häufigkeiten, auch deshalb, weil verschiedene Autoren ihre Untersuchungen für verschiedene Sprachen durchführten. Meist beginnt die Liste aber mit dem Leerzeichen (Blank) und „E” und endet mit Buchstaben wie „X”, „Y” und „Q”.

Zu obiger Tabelle ist zu bemerken:

• Die Entropie dieses Alphabets mit $M$ = 27 Zeichen wird $H$ ≈ 4 bit/Zeichen betragen. Wir haben das nicht nachgerechnet. Bacon hat aber schon 1623 einen Binärcode angegeben, bei dem jeder Buchstabe mit fünf Bit dargestellt wird: $L_M$ = 5.
• Etwa 250 Jahre danach hat Baudot diesen Code übernommen, der später auch für die gesamte Telegrafie standardisiert wurde. Eine ihm wichtige Überlegung war, dass ein Code mit einheitlich fünf Binärzeichen pro Buchstabe für einen Feind schwerer zu dechiffrieren ist, da dieser aus der Häufigkeit des Auftretens keine Rückschlüsse auf das übertragene Zeichen ziehen kann.
• Die letzte Zeile gibt einen beispielhaften Huffman–Code für obige Häufigkeitsverteilung an. Wahrscheinliche Zeichen wie „E” oder „N” und auch das „Blank” werden mit nur drei Bit dargestellt, das seltene „Q” dagegen mit 11 Bit. Die mittlere Codewortlänge ist geringfügig größer als $H$ ⇒ $L_M$ = $H + ε$, wobei wir uns hier über das $ε$ nicht auslassen wollen. Nur soviel: Es gibt keinen präfixfreien Code mit kleinerer mittlerer Wortlänge als den Huffman–Code.
• Auch Samuel Morse berücksichtigte bereits bei seinem Code für die Telegrafie in den 1830er Jahren die unterschiedlichen Häufigkeiten. Der Morse–Code eines jeden Zeichens besteht aus zwei bis vier Binärzeichen, die hier entsprechend der Anwendung mit Punkt („Kurz”) und Strich („Lang”) bezeichnet werden.
• Es ist offensichtlich, dass für den Morsecode $L_M$ < 4 gelten wird. Dies hängt aber auch damit zusammen, dass dieser nicht präfixfrei ist. Zwischen jeder Kurz–Lang–Sequenz musste deshalb der Funker eine Pause einlegen, damit die Gegenstation das Funksignal auch entschlüsseln konnte.