Aufgabe 2.4: 2D-Übertragungsfunktion
Aus LNTwww
Version vom 19. November 2017, 11:47 Uhr von Hussain (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „ {{quiz-Header|Buchseite=Mobile Kommunikation/Mehrwegeempfang beim Mobilfunk}} Datei:P_ID2161__Mob_A_2_4.png|right|frame|2D–Impulsantwort |<i>h</i>(<i>τ<…“)
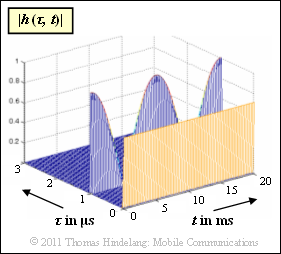
Dargestellt ist die zweidimensionale Impulsantwort $h(\tau, t)$ eines Mobilfunksystems in Betragsdarstellung. Es ist zu erkennen, dass die 2D–Impulsantwort nur für die Verzögerungszeiten $\tau = 0$ und $\tau = 1 \ \rm \mu s$ Anteile besitzt. Zu diesen Zeitpunkten gilt:
- $$h(\tau = 0\,{\rm \mu s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{1}{ \sqrt{2}} = {\rm const.}$$
- $$h(\tau = 1\,{\rm \mu s},\hspace{0.05cm}t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \cos(2\pi \cdot {t}/{ T_0})\hspace{0.05cm}.$$
Für alle anderen $\tau$–Werte ist $h(\tau, t) = 0$.
Gesucht ist die zweidimensionale Übertragungsfunktino $H(f, t)$ als die Fouriertransformierte von $h(\tau, t)$ hinsichtlich der Verzögerungszeit $\tau$:
- $$H(f,\hspace{0.05cm} t) \hspace{0.2cm} \stackrel {f,\hspace{0.05cm}\tau}{\bullet\!\!-\!\!\!-\!\!\!-\!\!\circ} \hspace{0.2cm} h(\tau,\hspace{0.05cm}t) \hspace{0.05cm}.$$
Hinweise:
- Die Aufgabe gehört zum Kapitel Mehrwegeempfang beim Mobilfunk.
- Eine ähnliche Problematik wird in der Aufgabe A2.5 behandelt, allerdings mit veränderter Nomenklatur.
Fragebogen
Musterlösung
(1)
(2)
(3)
(4)
(5)