Matched-Filter
Inhaltsverzeichnis
Optimierungskriterium des Matched–Filters
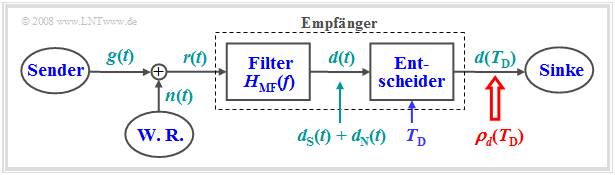
Das Matched-Filter – auch Korrelationsfilter genannt – dient zum Nachweis der Signalexistenz. Es kann mit größtmöglicher Sicherheit – anders ausgedrückt: mit maximalem SNR – entscheiden, ob ein durch additives Rauschen $n(t)$ gestörtes impulsförmiges Nutzsignal $g(t)$ vorhanden ist oder nicht. Zur Herleitung des Matched-Filters wird folgende Anordnung betrachtet.
Für die einzelnen Komponenten gelten folgende Voraussetzungen:
- Der Nutzanteil $g(t)$ des Empfangssignals $r(t)$ sei impulsförmig und somit energiebegrenzt. Das heißt: Das Integral über $g^2(t)$ von $–∞$ bis $+∞$ liefert den endlichen Wert $E_g$.
- Das Störsignal $n(t)$ sei Weißes Gaußsches Rauschen mit der Rauschleistungsdichte $N_0$.
- Das Filterausgangssignal $d(t)$ setzt sich additiv aus zwei Anteilen zusammen. Der Anteil $d_{\rm S}(t)$ geht auf das $\rm S$ignal $g(t)$ zurück und der Anteil $d_{\rm N}(t)$ auf das $\rm N$oise $n(t)$.
- Der Empfänger, bestehend aus einem linearen Filter ⇒ Frequenzgang $H_{\rm MF}(f)$ und dem Entscheider, ist so zu dimensionieren, dass das momentane S/N-Verhältnis am Ausgang maximal wird:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {d_{\rm S} ^2 ( {T_{\rm D} } )} }{ {\sigma _d ^2 } }\mathop = \limits^{\rm{!} }\hspace{0.1cm} {\rm{Maximum} }.$$
- Hierbei bezeichnen $σ_d^2$ die Varianz (Leistung) von $d_{\rm N}(t)$ und $T_{\rm D}$ den (geeignet gewählten) Detektionszeitpunkt.
Matched-Filter-Optimierung
Gegeben sei ein energiebegrenztes Nutzsignal $g(t)$ mit dem zugehörigen Spektrum $G(f)$. Damit kann das Filterausgangssignal zum Detektionszeitpunkt $T_{\rm D}$ für jedes beliebige Filter mit der Impulsantwort $h(t)$ und dem Frequenzgang $H(f) =\mathcal{ F}${ $h(t)$} wie folgt geschrieben werden (ohne Berücksichtigung des Rauschens ⇒ Index $\rm $S für „Signal”):
- $$d_{\rm S} ( {T_{\rm D} } ) = g(t) * h(t) = \int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e}}^{{\rm{j}}2{\rm{\pi }}fT_{\rm D} }\hspace{0.1cm} {\rm{d}}f} .$$
Der „Rauschanteil” $d_{\rm N}(t)$ des Filterausgangssignals (Index $\rm N$ für „Noise”) rührt allein vom Weißen Rauschen $n(t)$ am Eingang des Empfängers her. Für seine Varianz (Leistung) gilt unabhängig vom Detektionszeitpunkt $T_{\rm D}$:
- $$\sigma _d ^2 = \frac{ {N_0 } }{2} \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
Damit lautet das hier vorliegende Optimierungsproblem:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left| {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{{\rm{j} }2{\rm{\pi } }fT_{\rm D} }\hspace{0.1cm} {\rm{d} }f} } \right|^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left| {H(f)} \right|^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } \stackrel{!}{=} {\rm{Maximum} }.$$
$\text{Hier ohne Beweis:}$ Man kann zeigen, dass der Quotient für den folgenden Frequenzgang am größten wird:
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm e}^{- {\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\pi \hspace{0.05cm}\cdot \hspace{0.05cm}f \hspace{0.05cm}\cdot \hspace{0.05cm}T_{\rm D} } . $$
- Damit erhält man für das Signal-zu-Rauschleistungsverhältnis am Matched–Filter–Ausgang (und zwar unabhängig von der dimensionsbehafteten Konstante $K_{\rm MF}$):
- $$\rho _d ( {T_{\rm D} } ) = { {2 \cdot E_g } }/{ {N_0 } }.$$
- $E_g$ bezeichnet die Energie des Eingangsimpulses, die man nach dem Satz von Parseval sowohl im Zeit– als auch im Frequenzbereich berechnen kann:
- $$E_g = \int_{ - \infty }^{ + \infty } {g^2 (t)\hspace{0.1cm}{\rm{d} }t} = \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right\vert ^{\rm{2} }\hspace{0.1cm} {\rm d}f} .$$
$\text{Beispiel 1:}$ Ein rechteckförmiger Impuls $g(t)$ mit der Amplitude $\rm 1\hspace{0.05cm}V$ und der Dauer $0.5\hspace{0.05cm} \rm ms$ und unbekannter Lage soll in einer verrauschten Umgebung aufgefunden werden. Somit ist die Impulsenergie $E_g = \rm 5 · 10^{–4} \hspace{0.05cm}V^2s$. Die Rauschleistungsdichte sei $N_0 = \rm 10^{–6} \hspace{0.05cm}V^2/Hz$.
Das beste Ergebnis ⇒ das maximale S/N–Verhältnis erzielt man mit dem Matched-Filter:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {2 \cdot E_g } }{ {N_0 } } = \frac{ {2 \cdot 5 \cdot 10^{-4}\, {\rm V^2\,s} } }{ {10^{-6}\, {\rm V^2/Hz} } } = 1000 \hspace{0.3cm}\Rightarrow\hspace{0.3cm} 10 \cdot {\rm lg}\hspace{0.15cm}\rho _d ( {T_{\rm D} } ) = 30\,{\rm dB}.$$
Das oben angegebene Matched–Filter–Kriterium wird nun schrittweise hergeleitet. Wenn Sie daran nicht interessiert sind, so springen Sie bitte zur Fortsetzungsseite Interpretation des Matched–Filters.
$\text{Herleitung des Matched–Filter–Kriteriums:}$ Die Schwarzsche Ungleichung lautet mit den beiden (im allgemeinen komplexen) Funktionen $A(f)$ und $B(f)$:
- $$\left \vert {\int_a^b {A(f) \cdot B(f)\hspace{0.1cm}{\rm{d} }f} } \right \vert ^2 \le \int_a^b {\left \vert {A(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} \cdot \int_a^b {\left\vert {B(f)} \right \vert^{\rm{2} } \hspace{0.1cm}{\rm{d} }f} .$$
Wir wenden nun diese Gleichung auf das Signal–zu–Rauschverhältnis an:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert {\int_{ - \infty }^{ + \infty } {G(f) \cdot H(f) \cdot {\rm{e} }^{ {\rm{j} }2{\rm{\pi } }fT_{\rm D} } \hspace{0.1cm}{\rm{d} }f} } \right \vert^2 } }{ {N_0 /2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {H(f)} \right \vert^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } }.$$
Mit $A(f) = G(f)$ und $B(f) = H(f) · {\rm e}^{ {\rm j2}πfT_{\rm D} }$ ergibt sich somit die folgende Schranke:
- $$\rho_d ( {T_{\rm D} } ) \le \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert^{\rm{2} } }\hspace{0.1cm}{\rm{d} }f .$$
Setzt man für den Filterfrequenzgang versuchsweise
- $$H(f) = H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} }$$
ein, so erhält man aus der obigen Gleichung:
- $$\rho _d ( {T_{\rm D} } ) = \frac{ {\left \vert K_{\rm MF}\cdot {\int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } \right \vert ^2 } }{ {N_0 /2 \cdot K_{\rm MF} ^2 \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} } } = \frac{1}{ {N_0 /2} } \cdot \int_{ - \infty }^{ + \infty } {\left \vert {G(f)} \right \vert ^{\rm{2} }\hspace{0.1cm} {\rm{d} }f} .$$
Das heißt:
- Mit diesem Ansatz für das Matched-Filter $H_{\rm MF}(f)$ wird in obiger Abschätzung tatsächlich der maximal mögliche Wert erreicht.
- Mit keinem anderen Filter $H(f) ≠ H_{\rm MF}(f)$ kann man ein höheres Signal–zu–Rauschleistungsverhältnis erzielen.
- Das Matched–Filter ist in Bezug auf das ihm zugrunde gelegte Maximierungskriterium optimal.
Interpretation des Matched-Filters
Auf der letzten Seite wurde der Frequenzgang des Matched-Filters wie folgt hergeleitet:
- $$H_{\rm MF} (f) = K_{\rm MF} \cdot G^{\star} (f) \cdot {\rm{e} }^{ {\rm{ - j} }2{\rm{\pi } }fT_{\rm D} } .$$
Durch Fourierrücktransformation erhält man die dazugehörige Impulsantwort:
- $$h_{\rm MF} (t) = K_{\rm MF} \cdot g(T_{\rm D} - t).$$
Diese beiden Funktionen lassen sich wie folgt interpretieren:
- Das Matched-Filter ist durch den Term $G^{\star}(f)$ an das Spektrum des aufzufindenden Impulses $g(t)$ angepasst – daher sein Name (englisch: to match ≡ anpassen).
- Die Konstante $K_{\rm MF}$ ist aus Dimensionsgründen notwendig. Ist $g(t)$ ein Spannungsimpuls, so hat diese Konstante die Einheit „Hz/V”. Der Frequenzgang ist somit dimensionslos.
- Die Impulsantwort $h_{\rm MF}(t)$ ergibt sich aus dem Nutzsignal $g(t)$ durch Spiegelung ⇒ aus $g(t)$ wird $g(–t)$ – sowie einer Verschiebung um $T_{\rm D}$ nach rechts.
- Der früheste Detektionszeitpunkt $T_{\rm D}$ folgt für realisierbare Systeme aus der Bedingung $h_{\rm MF}(t < 0)$ ≡ 0 ⇒ „Kausalität” (siehe Buch Lineare zeitinvariante Systeme ).
- Der Nutzanteil $d_{\rm S} (t)$ des Filterausgangssignals ist formgleich mit der Energie-AKF (in diesem Tutorial durch einen Punkt gekennzeichnet) und gegenüber dieser um $T_{\rm D}$ verschoben. Es gilt:
- $$d_{\rm S} (t) = g(t) * h_{\rm MF} (t) = K_{\rm MF} \cdot g(t) * g(T_{\rm D} - t) = K_{\rm MF} \cdot \varphi^{^{\bullet} }_{g} (t - T_{\rm D} ).$$
$\text{Bitte beachten Sie:}$ Bei einem energiebegrenzten Signal $g(t)$ kann man nur die Energie–AKF angeben:
- $$\varphi^{^{\bullet} }_g (\tau ) = \int_{ - \infty }^{ + \infty } {g(t) \cdot g(t + \tau )\,{\rm{d} }t} .$$
Gegenüber der AKF-Definition eines leistungsbegrenzten Signals $x(t)$, nämlich
- $$\varphi _x (\tau ) = \mathop {\lim }_{T_{\rm M} \to \infty } \frac{1}{ {T_{\rm M} } }\int_{ - T_{\rm M} /2}^{+T_{\rm M} /2} {x(t) \cdot x(t + \tau )\hspace{0.1cm}\,{\rm{d} }t} ,$$
wird bei der Berechnung der Energie-AKF auf die Division durch die Messdauer $T_{\rm M}$ sowie auf den Grenzübergang $T_{\rm M} → ∞$ verzichtet.
$\text{Beispiel 2:}$ Wir gehen wieder davon aus, dass der Rechteckimpuls zwischen $\rm 2\hspace{0.05cm}ms$ und $\rm 2.5\hspace{0.05cm}ms$ liegt und der Detektionszeitpunkt $T_{\rm D} =\rm 2\hspace{0.05cm}ms$ gewünscht wird. Dann gilt:
- Die Matched–Filter–Impulsantwort $h_{\rm MF}(t)$ muss im Bereich von $t_1 (= 4 – 2.5) =\rm 1.5\hspace{0.05cm}ms$ bis $t_2 (= 4 – 2) =\rm 2\hspace{0.05cm}ms$ konstant sein. Für $t < t_1$ sowie für $t > t_2$ darf sie keine Anteile besitzen.
- Der Betragsfrequenzgang $\vert H_{\rm MF}(f)\vert$ ist hier si–förmig. Die Höhe der Impulsantwort $h_{\rm MF}(t)$ spielt für das S/N–Verhältnis keine Rolle, da dieses unabhängig von $K_{\rm MF}$ ist.
Verallgemeinertes Matched-Filter für den Fall farbiger Störungen
Bei den Herleitungen dieses Abschnittes wurde bisher stets von Weißem Rauschen ausgegangen. Nun soll die Frage geklärt werden, wie das Empfangsfilter $H(f) = H_{\rm MF}(f)$ bei farbiger Störung $n(t)$ zu gestalten ist, damit das Signal–zu–Rauschleistungsverhältnis maximal wird.
$\text{Zur Erläuterung einiger Begrifflichkeiten:}$ Dere Begriff „Störung” ist etwas allgemeiner als „Rauschen”. Vielmehr ist Rauschen eine Teilmenge aller Störungen, zu denen zum Beispiel auch das Nebensprechen von benachbarten Leitungen zählt.
- Wir sprechen nur dann von (weißem) Rauschen $n(t)$, wenn das Leistungsdichtespektrum ${\it Φ}_n(f)$ für alle Frequenzen gleich ist.
- Ist dies nicht erfüllt, so bezeichnen wir $n(t)$ als farbige Störung.
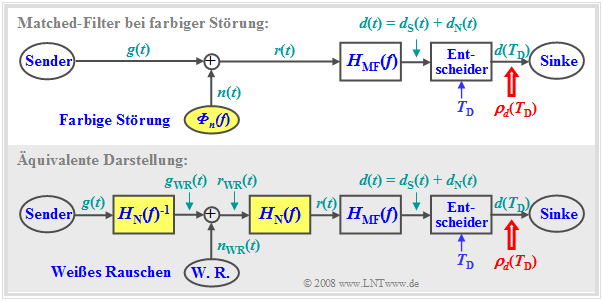
Zum hier betrachteten Modell ist anzumerken:
- Die obere Grafik zeigt das Blockschaltbild zur Herleitung des Matched–Filters $H_{\rm MF}(f)$ bei farbiger Störung $n(t)$, gekennzeichnet durch das Leistungsdichtespektrum ${\it Φ}_n(f) ≠$ const. Alle bisher für diesen Abschnitt genannten Voraussetzungen gelten weiterhin.
- Das farbige Störsignal $n(t)$ mit dem Leistungsdichtespektrum ${\it Φ}_n(f)$ kann man – zumindest gedanklich – durch eine „weiße” Rauschquelle $n_{\rm WR}(t)$ mit der konstanten (zweiseitigen) Rauschleistungsdichte $N_0/2$ und ein Formfilter mit dem Frequenzgang $H_{\rm N}(f)$ modellieren:
- $${\it{\Phi} }_n \left( f \right) = { {N_{\rm 0} } }/{\rm 2} \cdot \left| {H_{\rm N} \left( f \right)} \right|^{\rm 2} .$$
- Diese Modifikation ist in der unteren (der obigen) Grafik berücksichtigt. Da Realisierungsaspekte hier nicht betrachtet werden, wird $H_{\rm N}(f)$ vereinfacht als reell angenommen. Der Phasengang von $H_{\rm N}(f)$ spielt für das Folgende keine Rolle.
- In dieser Darstellung ist zudem das Formfilter $H_{\rm N}(f)$ auf die rechte Seite der Störaddition verschoben. Um ein auch bezüglich des Nutzsignals $d_{\rm S}(t)$ äquivalentes Modell zu erhalten, wird das Formfilter im Nutzsignalzweig durch das inverse Filter $H_{\rm N}(f)^{–1}$ kompensiert.
Anhand dieses modifizierten Modells wird nun das Matched-Filter für den Fall farbiger Störungen hergeleitet. Besitzt $H_{\rm N}(f)$ keine Nullstelle, was für das Folgende vorausgesetzt werden soll, so ist diese Anordnungen mit dem obigen Blockschaltbild identisch.
An der Störadditionsstelle liegt nun weißes Rauschen $n_{\rm WR}(t)$ an. Die Herleitung der Matched–Filter–Optimierung bei weißem Rauschen lässt sich in einfacher Weise auf das aktuelle Problem anpassen, wenn man Folgendes berücksichtigt:
- Anstelle des tatsächlichen Sendesignals $g(t)$ ist das Signal $g_{\rm WR}(t)$ vor der Störaddition zu berücksichtigen. Die dazugehörige Spektralfunktion lautet: $G_{\rm WR}(f) = G(f)/H_{\rm N}(f)$.
- Anstelle von $H_{\rm MF}(f)$ ist nun der resultierende Frequenzgang ${H_{\rm MF} }' (f) = H_{\rm N}(f) · H_{\rm MF}$ rechts von der Störadditionsstelle einzusetzen.
$\text{Fazit:}$
(1) Für das Matched-Filter bei farbigen Störungen ergibt sich:
- $${H_{\rm MF} }\hspace{0.01cm}' (f) = H_{\rm N} (f) \cdot H_{\rm MF} (f) = K_{\rm MF} \cdot G_{\rm WR} ^ {\star} (f) \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm D} } \hspace{0.3cm}\Rightarrow \hspace{0.3cm}H_{\rm MF} (f) = K_{\rm MF} \cdot \frac{ {G^{\star} (f)} }{ {\left\vert {H_{\rm N} (f)} \right\vert^2 } } \cdot {\rm{e} }^{ - {\rm{j} }2{\rm{\pi } }fT_{\rm D} } .$$
(2) Das Signal-zu-Störleistungsverhältnis vor dem Entscheider ist somit maximal:
- $$\rho _{d,\max } ( {T_{\rm D} } ) = \frac{1}{ {N_0 /2} }\int_{ - \infty }^{ + \infty } {\left\vert{G_{\rm WR} (f)} \right\vert^2 }\, {\rm{d} }f = \int_{ - \infty }^{ + \infty } \frac{\left \vert G(f) \right\vert^2 }{ {\it{\Phi _n {\rm (f)} } } } \,{\rm{d} }f.$$
(3) Der Fall „Weißes Rauschen” ist in dieser allgemeineren Gleichung für ${\it Φ}_n(f) = N_0/2$ mitenthalten.
(4) Alle hier angegebenen Gleichungen führen bei farbiger Störung allerdings nur dann zu sinnvollen, auch in der Praxis verwertbaren Ergebnissen, wenn das Energiespektrum $\vert G(f)\vert ^2$ des Nutzsignals asymptotisch schneller abklingt als das Störleistungsdichtespektrum ${\it Φ}_n(f)$.
Aufgaben zum Kapitel
Aufgabe 5.7: Rechteck-Matched-Filter
Aufgabe 5.7Z: Matched-Filter - alles gaußisch
Aufgabe 5.8: Matched-Filter für farbige Störung
Aufgabe 5.8Z: Matched-Filter bei Rechteck-LDS