Kapazität von digitalen gedächtnislosen Kanälen
Inhaltsverzeichnis
Programmbeschreibung
In diesem Applet werden binäre $(M=2)$ und ternäre $(M=3)$ Kanalmodelle ohne Gedächtnis betrachtet mit jeweils $M$ Eingängen $X$ und $M$ Ausgängen $Y$. Ein solches Nachrichtensystem ist durch die Wahrscheinlichkeitsfunktion $P_X(X)$ und die Matrix $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ der Übergangswahrscheinlichkeiten vollständig bestimmt.
Für diese binären bzw. ternären Systeme werden folgende informationstheoretische Beschreibungsgrößen hergeleitet und verdeutlicht:
- die Quellenentropie $H(X)$ und die Sinkenentropie $H(Y)$,
- die Äquivokation („Rückschlussentropie”) $H(X|Y)$ und die Irrelevanz („Streuentropie”) $H(Y|X)$,
- die Verbundentropie $H(XY)$ sowie die Transinformation (englisch: Mutual Information) $I(X; Y)$,
- die Kanalkapazität als die entscheidende Kenngröße digitaler Kanalmodelle ohne Gedächtnis:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Diese informationstheoretische Größen können sowohl in analytische geschlossener Form berechnet oder durch Auswertung von Quellen– und Sinkensymbolfolge simulativ ermittelt werden.
Theoretischer Hintergrund
Zugrunde liegendes Modell der Digitalsignalübertragung
Die Menge der möglichen Quellensymbole wird durch die diskrete Zufallsgröße $X$ charakterisiert.
- Im binären Fall ⇒ $M_X= |X| = 2$ gilt $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B} \hspace{0.05cm}\}$ mit der Wahrscheinlichkeitsfunktion $($englisch: Probability Mass Function, $\rm PMF)$ $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B}\big)$ sowie den Quellensymbolwahrscheinlichkeiten $p_{\rm A}$ und $p_{\rm B}=1- p_{\rm A}$.
- Entsprechend gilt für eine Ternärquelle ⇒ $M_X= |X| = 3$: $X = \{\hspace{0.05cm}{\rm A}, \hspace{0.15cm} {\rm B}, \hspace{0.15cm} {\rm C} \hspace{0.05cm}\}$, $P_X(X)= \big (p_{\rm A},\hspace{0.15cm}p_{\rm B},\hspace{0.15cm}p_{\rm C}\big)$, $p_{\rm C}=1- p_{\rm A}-p_{\rm B}$.
Die Menge der möglichen Sinkensymbole wird durch die diskrete Zufallsgröße $Y$ charakterisiert. Diese entstammen der gleichen Symbolmenge wie die Quellensymbole ⇒ $M_Y=M_X = M$. Zur Vereinfachung der nachfolgenden Beschreibung bezeichnen wir diese mit Kleinbuchstaben, zum Beispiel für $M=3$: $Y = \{\hspace{0.05cm}{\rm a}, \hspace{0.15cm} {\rm b}, \hspace{0.15cm} {\rm c} \hspace{0.05cm}\}$.
Der Zusammenhang zwischen den Zufallsgrößen $X$ und $Y$ ist durch ein digitales Kanalmodell ohne Gedächtnis $($englisch: Discrete Memoryless Channel, $\rm DMC)$ festgelegt. Die linke Grafik zeigt dieses für $M=2$ und die rechte Grafik für $M=3$.
Die folgende Beschreibung gilt für den einfacheren Fall $M=2$. Für die Berechnung aller informationstheoretischer Größen im nächsten Abschnitt benötigen wir außer $P_X(X)$ und $P_Y(Y)$ noch die zweidimensionalen Wahrscheinlichkeitsfunktionen $($jeweils eine $2\times2$–Matrix$)$ aller
- bedingten Wahrscheinlichkeiten ⇒ $P_{\hspace{0.01cm}Y\hspace{0.03cm} \vert \hspace{0.01cm}X}(Y\hspace{0.03cm} \vert \hspace{0.03cm} X)$ ⇒ durch das DMC–Modell vorgegeben;
- Verbundwahrscheinlichkeiten ⇒ $P_{XY}(X,\hspace{0.1cm}Y)$;
- Rückschlusswahrscheinlichkeiten ⇒ $P_{\hspace{0.01cm}X\hspace{0.03cm} \vert \hspace{0.03cm}Y}(X\hspace{0.03cm} \vert \hspace{0.03cm} Y)$.
$\text{Beispiel 1}$: Wir betrachten den skizzierten Binärkanal.
- Die Verfälschungswahrscheinlichkeiten seien:
- $$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\ p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) = \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} \hspace{0.05cm}.$$
- Außerdem gehen wir von nicht gleichwahrscheinlichen Quellensymbolen aus:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$
- Für die Wahrscheinlichkeitsfunktion der Sinke ergibt sich somit:
- $$P_Y(Y) = \big [ {\rm Pr}( Y\hspace{-0.1cm} = {\rm a})\hspace{0.05cm}, \ {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) \big ] = \big ( 0.1\hspace{0.05cm},\ 0.9 \big ) \cdot \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} $$
- $$\Rightarrow \hspace{0.3cm} {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) = 0.1 \cdot 0.95 + 0.9 \cdot 0.4 = 0.455\hspace{0.05cm},\hspace{1.0cm} {\rm Pr}( Y \hspace{-0.1cm}= {\rm b}) = 1 - {\rm Pr}( Y \hspace{-0.1cm}= {\rm a}) = 0.545.$$
- Die Verbundwahrscheinlichkeiten $p_{\mu \kappa} = \text{Pr}\big[(X = μ) ∩ (Y = κ)\big]$ zwischen Quelle und Sinke sind:
- $$\begin{align*}p_{\rm Aa} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.095\hspace{0.05cm},\hspace{0.5cm}p_{\rm Ab} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = 0.005\hspace{0.05cm},\\ p_{\rm Ba} & = p_{\rm a} \cdot p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.360\hspace{0.05cm}, \hspace{0.5cm}p_{\rm Bb} = p_{\rm b} \cdot p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = 0.540\hspace{0.05cm}. \end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{XY}(X,\hspace{0.1cm}Y) = \begin{pmatrix} 0.095 & 0.005\\ 0.36 & 0.54 \end{pmatrix} \hspace{0.05cm}.$$
- Für die Rückschlusswahrscheinlichkeiten erhält man:
- $$\begin{align*}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Aa}/p_{\rm a} = 0.095/0.455 = 0.2088\hspace{0.05cm},\hspace{0.5cm}p_{\rm A\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Ab}/p_{\rm b} = 0.005/0.545 = 0.0092\hspace{0.05cm},\\ p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}a} & = p_{\rm Ba}/p_{\rm a} = 0.36/0.455 = 0.7912\hspace{0.05cm},\hspace{0.5cm}p_{\rm B\hspace{0.03cm}\vert \hspace{0.03cm}b} = p_{\rm Bb}/p_{\rm b} = 0.54/0.545 = 0.9908\hspace{0.05cm} \end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}X\hspace{0.05cm} \vert \hspace{0.05cm}Y}(X\hspace{0.05cm} \vert \hspace{0.05cm} Y) = \begin{pmatrix} 0.2088 & 0.0092\\ 0.7912 & 0.9908 \end{pmatrix} \hspace{0.05cm}.$$
Definition und Interpretation verschiedener Entropiefunktionen
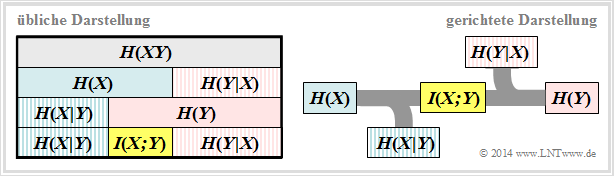
Im $\rm LNTwww$–Theorieteil werden alle für 2D–Zufallsgrößen relevanten Entropien definiert, die auch für die Digitalsignalübertragung gelten. Zudem finden Sie dort zwei Schaubilder, die den Zusammenhang zwischen den einzelnen Entropien illustrieren.
- Für die Digitalsignalübertragung ist die rechte Darstellung zweckmäßig, bei der die Richtung von der Quelle $X$ zur Sinke $Y$ erkennbar ist.
- Wir interpretieren nun ausgehend von dieser Grafik die einzelnen informationstheoretischen Größen.
- Die Quellenentropie (englisch: Source Entropy ) $H(X)$ bezeichnet den mittleren Informationsgehalt der Quellensymbolfolge. Mit dem Symbolumfang $|X|$ gilt:
- $$H(X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(X)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_X(X)}\big ] \hspace{0.2cm} =\hspace{0.2cm} \sum_{\mu = 1}^{|X|} P_X(x_{\mu}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_X(x_{\mu})} \hspace{0.05cm}.$$
- Die Äquivokation (auch Rückschlussentropie genannt, englisch: Equivocation ) $H(X|Y)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Sinke $Y$ genau Bescheid weiß, durch Beobachtung der Quelle $X$ gewinnt:
- $$H(X|Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{-0.01cm}Y}(X\hspace{-0.01cm} |\hspace{0.03cm} Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}X\hspace{-0.01cm}|\hspace{0.03cm}Y} (\hspace{0.05cm}x_{\mu}\hspace{0.03cm} |\hspace{0.05cm} y_{\kappa})} \hspace{0.05cm}.$$
- Die Äquivokation ist der Anteil der Quellenentropie $H(X)$, der durch Kanalstörungen (bei digitalem Kanal: Übertragungsfehler) verloren geht. Es verbleibt die Transinformation (englisch: Mutual Information) $I(X; Y)$, die zur Sinke gelangt:
- $$I(X;Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(X, Y)}{P_X(X) \cdot P_Y(Y)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa})}{P_{\hspace{0.05cm}X}(\hspace{0.05cm}x_{\mu}) \cdot P_{\hspace{0.05cm}Y}(\hspace{0.05cm}y_{\kappa})} \hspace{0.05cm} = H(X) - H(X|Y) \hspace{0.05cm}.$$
- Die Irrelevanz (manchmal auch Streuentropie genannt, englisch: Irrelevance) $H(Y|X)$ gibt den mittleren Informationsgehalt an, den ein Betrachter, der über die Quelle $X$ genau Bescheid weiß, durch Beobachtung der Sinke $Y$ gewinnt:
- $$H(Y|X) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{-0.01cm}X}(Y\hspace{-0.01cm} |\hspace{0.03cm} X)}\right ] \hspace{0.2cm}=\hspace{0.2cm} \sum_{\mu = 1}^{|X|} \sum_{\kappa = 1}^{|Y|} P_{XY}(x_{\mu},\hspace{0.05cm}y_{\kappa}) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}|\hspace{0.03cm}X} (\hspace{0.05cm}y_{\kappa}\hspace{0.03cm} |\hspace{0.05cm} x_{\mu})} \hspace{0.05cm}.$$
- Die Sinkenentropie $H(Y)$, der mittlere Informationsgehalt der Sinke, ist die Summe aus der nützlichen Transinformation $I(X; Y)$ und der Irrelevanz $H(Y|X)$, die ausschließlich von Kanalfehlern herrührt:
- $$H(Y) = {\rm E} \left [ {\rm log}_2 \hspace{0.1cm} \frac{1}{P_Y(Y)}\right ] \hspace{0.1cm} = -{\rm E} \big [ {\rm log}_2 \hspace{0.1cm}{P_Y(Y)}\big ] \hspace{0.2cm} =I(X;Y) + H(Y|X) \hspace{0.05cm}.$$
- Die Verbundentropie $H(XY)$ gibt ist den mittleren Informationsgehalt der 2D–Zufallsgröße $XY$ an.  sie beschreibt zudem eine obere Schranke für die Summe aus Quellenentropie und Sinkenentropie:
- $$H(XY) = {\rm E} \left [ {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(X, Y)}\right ] = \sum_{\mu = 1}^{M} \hspace{0.1cm} \sum_{\kappa = 1}^{K} \hspace{0.1cm} P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa}) \cdot {\rm log} \hspace{0.1cm} \frac{1}{P_{XY}(x_{\mu}\hspace{0.05cm}, y_{\kappa})}\le H(X) + H(Y) \hspace{0.05cm}.$$
$\text{Beispiel 2}$: Es gelten die gleichen Voraussetzungen wie für das $\text{Beispiel 1}$:
(1) Die Quellensymbole sind nicht gleichwahrscheinlich:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B} \big )= \big ( 0.1,\ 0.9 \big ) \hspace{0.05cm}.$$
(2) Die Verfälschungswahrscheinlichkeiten seien:
- $$\begin{align*}p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.95\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm A}) = 0.05\hspace{0.05cm},\\ p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} & = {\rm Pr}(Y\hspace{-0.1cm} = {\rm a}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.40\hspace{0.05cm},\hspace{0.8cm}p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = {\rm Pr}(Y\hspace{-0.1cm} = {\rm b}\hspace{0.05cm}\vert X \hspace{-0.1cm}= {\rm B}) = 0.60\end{align*}$$
- $$\Rightarrow \hspace{0.3cm} P_{\hspace{0.01cm}Y\hspace{0.05cm} \vert \hspace{0.05cm}X}(Y\hspace{0.05cm} \vert \hspace{0.05cm} X) = \begin{pmatrix} 0.95 & 0.05\\ 0.4 & 0.6 \end{pmatrix} \hspace{0.05cm}.$$
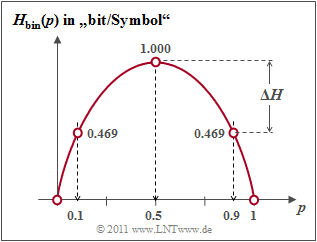
- Wegen Voraussetzung (1) erhält man so für die Quellenentropie mit der binären Entropiefunktion $H_{\rm bin}(p)$:
- $$H(X) = p_{\rm A} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm A}\hspace{0.1cm} } + p_{\rm B} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{p_{\rm B} }= H_{\rm bin} (p_{\rm A}) = H_{\rm bin} (0.1)= 0.469 \ {\rm bit} \hspace{0.05cm};$$
- $$H_{\rm bin} (p) = p \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p\hspace{0.1cm} } + (1 - p) \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{1 - p} \hspace{0.5cm}{\rm (Einheit\hspace{-0.15cm}: \hspace{0.15cm}bit\hspace{0.15cm}oder\hspace{0.15cm}bit/Symbol)} \hspace{0.05cm}.$$
- Entsprechend gilt für die Sinkenentropie mit der PMF $P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b} \big )= \big ( 0.455,\ 0.545 \big )$:
- $$H(Y) = H_{\rm bin} (0.455)= 0.994 \ {\rm bit} \hspace{0.05cm}.$$
- Als nächstes berechnen wir die Verbundentropie:
- $$H(XY) = p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+ p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }+p_{\rm Ba} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ba}\hspace{0.1cm} }+ p_{\rm Bb} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Bb}\hspace{0.1cm} }$$
- $$\Rightarrow \hspace{0.3cm}H(XY) = 0.095 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.095 } +0.005 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.005 }+0.36 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.36 }+0.54 \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{0.54 }= 1.371 \ {\rm bit} \hspace{0.05cm}.$$
Entsprechend dem oberen linken Schaubild sind somit auch die restlichen informationstheoretischen Größen berechenbar:
- die Äquivokation (oder Rückschlussentropie):
- $$H(X \vert Y) \hspace{-0.01cm} =\hspace{-0.01cm} H(XY) \hspace{-0.01cm} -\hspace{-0.01cm} H(Y) \hspace{-0.01cm} = \hspace{-0.01cm} 1.371\hspace{-0.01cm} -\hspace{-0.01cm} 0.994\hspace{-0.01cm} =\hspace{-0.01cm} 0.377\ {\rm bit} \hspace{0.05cm},$$
- die Irrelevanz (oder Streuentropie):
- $$H(Y \vert X) = H(XY) - H(X) = 1.371 - 0.994 = 0.902\ {\rm bit} \hspace{0.05cm}.$$
- die Transinformation (englisch Mutual Information):
- $$I(X;Y) = H(X) + H(Y) - H(XY) = 0.469 + 0.994 - 1.371 = 0.092\ {\rm bit} \hspace{0.05cm},$$
Die Ergebnisse sind in nebenstehender Grafik zusammengefasst.
Anmerkung: Äquivokation und Irrelevanz könnte man (allerdfings mit Mehraufwand) auch direkt aus den entsprechenden Wahrscheinlichkeitsfunktionen berechnen, zum Beispiel:
- $$H(Y \vert X) = \hspace{-0.2cm} \sum_{(x, y) \hspace{0.05cm}\in \hspace{0.05cm}XY} \hspace{-0.2cm} P_{XY}(x,\hspace{0.05cm}y) \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{P_{\hspace{0.05cm}Y\hspace{-0.01cm}\vert \hspace{0.03cm}X} (\hspace{0.05cm}y\hspace{0.03cm} \vert \hspace{0.05cm} x)}= p_{\rm Aa} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} } + p_{\rm Ab} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} } + p_{\rm Ba} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}B} } + p_{\rm Bb} \cdot {\rm log}_2 \hspace{0.1cm} \frac{1}{p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} } = 0.902 \ {\rm bit} \hspace{0.05cm}.$$

Rote Übergänge stehen für $p_{\rm a\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}B} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}C} = q$ und blaue für $p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}A} = p_{\rm c\hspace{0.03cm}\vert \hspace{0.03cm}A} =\text{...}= p_{\rm b\hspace{0.03cm}\vert \hspace{0.03cm}C}= (1-q)/2$
$\text{Beispiel 3}$: Nun betrachten wir ein Übertragungssystem mit $M_X = M_Y = M=3$.
(1) Die Quellensymbole seien gleichwahrscheinlich:
- $$P_X(X) = \big ( p_{\rm A},\ p_{\rm B},\ p_{\rm C} \big )= \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(X)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit} \hspace{0.05cm}.$$
(2) Das Kanalmodell ist symmetrisch ⇒ auch die Sinkensymbole sind gleichwahrscheinlich:
- $$P_Y(Y) = \big ( p_{\rm a},\ p_{\rm b},\ p_{\rm c} \big )= \big ( 1/3,\ 1/3,\ 1/3 \big )\hspace{0.30cm}\Rightarrow\hspace{0.30cm}H(Y)={\rm log_2}\hspace{0.1cm}3 \approx 1.585 \ {\rm bit} \hspace{0.05cm}.$$
(3) Die Verbundwahrscheinlichkeiten ergeben sich wie folgt:
- $$p_{\rm Aa}= p_{\rm Bb}= p_{\rm Cc}= q/M,$$
- $$p_{\rm Ab}= p_{\rm Ac}= p_{\rm Ba}= p_{\rm Bc} = p_{\rm Ca}= p_{\rm Cb} = (1-q)/(2M)$$
- $$\Rightarrow\hspace{0.30cm}H(XY) = 3 \cdot p_{\rm Aa} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Aa}\hspace{0.1cm} }+6 \cdot p_{\rm Ab} \cdot {\rm log_2}\hspace{0.1cm}\frac{1}{\hspace{0.1cm}p_{\rm Ab}\hspace{0.1cm} }= \ \text{...} \ = q \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{q }+ (1-q) \cdot {\rm log_2}\hspace{0.1cm}\frac{M}{(1-q)/2 }.$$
(4) Für die Transinformation erhält man nach einigen Umformungen unter Berücksichtigung der Gleichung
- $$I(X;Y) = H(X) + H(Y) - H(XY)\text{:}$$
- $$I(X;Y) = {\rm log_2}\ (M) - (1-q) -H_{\rm bin}(q).$$
- Bei fehlerfreier Ternärübertragung $(q=1)$ gilt $I(X;Y) = H(X) = H(Y)={\rm log_2}\hspace{0.1cm}3$.
- Mit $q=0.8$ sinkt die Transinformaion schon auf $I(X;Y) = 0.663$ und mit $q=0.5$ auf $0.085$ bit.
- Der ungünstigste Fall aus informationstheoretischer Sicht ist $q=1/3$ ⇒ $I(X;Y) = 0$.
- Dagegen ist der aus der aus Sicht der Übertragungstheorie ungünstigste Fall $q=0$ ⇒ „kein einziges Übertragungssymbol kommt richtig an” aus informationstheoretischer Sicht gar nicht so schlecht.
- Um dieses gute Ergebnis nutzen zu können, ist allerdings sendeseitig eine Kanalcodierung erforderlich.
Definition und Bedeutung der Kanalkapazität
Berechnet man die Transinformation $I(X, Y)$ wie zuletzt im $\text{Beispiel 2}$ ausgeführt, so hängt diese nicht nur vom diskreten gedächtnislosen Kanal (englisch: Discrete Memoryless Channel, kurz DMC) ab, sondern auch von der Quellenstatistik ⇒ $P_X(X)$ ab. Ergo: Die Transinformation $I(X, Y)$ ist keine reine Kanalkenngröße.
$\text{Definition:}$ Die von Claude E. Shannon eingeführte Kanalkapazität (englisch: Channel Capacity) lautet gemäß seinem Standardwerk [Sha48][1]:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) \hspace{0.05cm}.$$
Oft wird die Zusatzeinheit „bit/Kanalzugriff” hinzugefügt, bei englischen Texten „bit/use”. Da nach dieser Definition stets die bestmögliche Quellenstatistik zugrunde liegt, hängt $C$ nur von den Kanaleigenschaften ⇒ $P_{Y \vert X}(Y \vert X)$ ab, nicht jedoch von der Quellenstatistik ⇒ $P_X(X)$.
Shannon benötigte die Kanalbeschreibungsgröße $C$ zur Formulierung des Kanalcodierungstheorems – eines der Highlights der von ihm begründeten Informationstheorie.
$\text{Shannons Kanalcodierungstheorem:}$
- Zu jedem Übertragungskanal mit der Kanalkapazität $C > 0$ existiert (mindestens) ein $(k, n)$–Blockcode, dessen (Block–)Fehlerwahrscheinlichkeit gegen Null geht, so lange die Coderate $R = k/n$ kleiner oder gleich der Kanalkapazität ist: $R ≤ C.$
- Voraussetzung hierfür ist allerdings, dass für die Blocklänge dieses Codes gilt: $n → ∞.$
$\text{Umkehrschluss von Shannons Kanalcodierungstheorem:}$
Ist die Rate $R$ des verwendeten $(n$, $k)$–Blockcodes größer als die Kanalkapazität $C$, so ist niemals eine beliebig kleine Blockfehlerwahrscheinlichkeit nicht erreichbar.
$\text{Beispiel 4}$: Wir betrachten den gleichen diskreten gedächtnislosen Kanal wie im $\text{Beispiel 2}$. In diesem $\text{Beispiel 2}$ wurden die Symbolwahrscheinlichkeiten $p_{\rm A} = 0.1$ und $p_{\rm B}= 1- p_{\rm A}=0.9$ vorausgesetzt. Damit ergab sich die Transinformation zu $I(X;Y)= 0.092$ bit/Kanalzugriff ⇒ siehe erste Zeile, vierte Spalte in der Tabelle.
Die Kanalkapazität ist die Transinformation $I(X, Y)$ bei bestmöglichen Symbolwahrscheinlichkeiten $p_{\rm A} = 0.55$ und $p_{\rm B}= 1- p_{\rm A}=0.45$:
- $$C = \max_{P_X(X)} \hspace{0.15cm} I(X;Y) = 0.284 \ \rm bit/Kanalzugriff \hspace{0.05cm}.$$
Aus der Tabelle erkennt man weiter (auf die Zusatzeinheit „bit/Kanalzugriff„ verzichten wir im Folgenden):
- Der Parameter $p_{\rm A} = 0.1$ war sehr ungünstig gewählt, weil beim vorliegenden Kanal das Symbol $\rm A$ mehr verfälscht wird als $\rm B$. Schon mit $p_{\rm A} = 0.9$ ergibt sich ein etwas besserer Wert: $I(X; Y)=0.130$.
- Aus dem gleichen Grund liefert $p_{\rm A} = 0.55$, $p_{\rm B} = 0.45$ ein etwas besseres Ergebnis als gleichwahrscheinliche Symbole $p_{\rm A} = p_{\rm B} =0.5$.
- Je unsymmetrischer der Kanal ist, um so mehr weicht die optimale Wahrscheinlichkeitsfunktion $P_X(X)$ von der Gleichverteilung ab. Im Umkehrschluss: Bei symmetrischem Kanal ergibt sich stets die Gleichverteilung.
Der Ternärkanal von $\text{Beispiel 3}$ ist symmetrisch. Deshalb ist hier $P_X(X) = \big ( 1/3,\ 1/3,\ 1/3 \big )$ für jeden $q$–Wert optimal, und die in der Ergebnistabelle angegebene Transinformation $I(X;Y)$ ist gleichzeitig die Kanalkapazität $C$.
Numerische Ermittlung der statistischen und informationstheoretischen Größen
mit einem Beispiel
Versuchsdurchführung
- Wählen Sie zunächst die Nummer 1 ... ? der zu bearbeitenden Aufgabe.
- Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
- Lösung nach Drücken von „Musterlösung”.
- Bei allen Entropiewerten müsste die Einheit "bit/use" hizugefügt werden.
- Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
(1) Es gelte $p_{\rm A} = p_{\rm B} = 0.5$ und $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$. Welches Kanalmodell liegt vor? Wie lauten die Entropien $H(X), \, H(Y)$ und die Transinformation $I(X;\, Y)$?
- Betrachtet wird das BSC–Modell (Binary Symmetric Channel). Wegen $p_{\rm A} = p_{\rm B} = 0.5$ gilt für die Quellen– und die Sinkenentropie: $H(X) = H(Y) = 1$.
- Wegen $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$ sind auch Äqivokation und Irrelevanz gleich: $H(X \vert Y) = H(Y \vert X) = H_{\rm bin}(p_{\rm b \vert A}) = H_{\rm bin}(0.1) =0.469$.
- Die Transinformation ist $I(X;\, Y) = H(X) - H(X \vert Y)= 1-H_{\rm bin}(p_{\rm b \vert A}) = 0.531$ und die Verbundentropie ist $H(XY) =1.469$.
(2) Es gelte weiter $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.1$, aber nun ist die Symbolwahrscheinlichkeit $p_{\rm A} = 0.9$. Wie groß ist die Kapazität $C_{\rm BSC}$ des BSC–Kanals mit $p_{\rm b \vert A} = p_{\rm a \vert B}$?
- Welches $p_{\rm b \vert A} = p_{\rm a \vert B}$ führt zur größtmöglichen Kanalkapazität und welches $p_{\rm b \vert A} = p_{\rm a \vert B}$ zur Kanalkapazität $C_{\rm BSC}=0$?
- Die Kapazität $C_{\rm BSC}$ ist gleich der maximalen Transinformation $I(X;\, Y)$ unter Berücksichtigung der optimalen Symbolwahrscheinlichkeiten.
- Aufgrund der Symmetrie des des BSC–Modells führen gleichwahrscheinliche Symbole $(p_{\rm A} = p_{\rm B} = 0.5)$ zum Optimum ⇒ $C_{\rm BSC}=0.531$.
- Am besten ist der ideale Kanal $(p_{\rm b \vert A} = p_{\rm a \vert B} = 0)$ ⇒ $C_{\rm BSC}=1$. Der schlechteste BSC–Kanal liegt durch $p_{\rm b \vert A} = p_{\rm a \vert B} = 0.5$ fest ⇒ $C_{\rm BSC}=0$.
(3) Es gelten weiter die Einstellungen von (1). Wie unterscheiden sich der Mittelwert $m_1$ und die Streuung $\sigma$ der beiden Binomialverteilungen?
- Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Mittelwert:}\hspace{0.2cm}m_\text{1} = I \cdot p\hspace{0.3cm} \Rightarrow\hspace{0.3cm} m_\text{1, Blau} = 5 \cdot 0.4\underline{ = 2 =} \ m_\text{1, Rot} = 10 \cdot 0.2; $
$\hspace{1.85cm}\text{Streuung:}\hspace{0.4cm}\sigma = \sqrt{I \cdot p \cdot (1-p)} = \sqrt{m_1 \cdot (1-p)}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \sigma_{\rm Blau} = \sqrt{2 \cdot 0.6} =1.095 < \sigma_{\rm Rot} = \sqrt{2 \cdot 0.8} = 1.265.$
(4) Setzen Sie Blau: Binomialverteilung $(I=15, p=0.3)$ und Rot: Poissonverteilung $(\lambda=4.5)$.
- Welche Unterschiede ergeben sich zwischen beiden Verteilungen hinsichtlich Mittelwert $m_1$ und Varianz $\sigma^2$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm}\text{Beide Verteilungern haben gleichen Mittelwert:}\hspace{0.2cm}m_\text{1, Blau} = I \cdot p\ = 15 \cdot 0.3\hspace{0.15cm}\underline{ = 4.5 =} \ m_\text{1, Rot} = \lambda$;
$\hspace{1.85cm} \text{Binomialverteilung: }\hspace{0.2cm} \sigma_\text{Blau}^2 = m_\text{1, Blau} \cdot (1-p)\hspace{0.15cm}\underline { = 3.15} \le \text{Poissonverteilung: }\hspace{0.2cm} \sigma_\text{Rot}^2 = \lambda\hspace{0.15cm}\underline { = 4.5}$;
(5) Es gelten die Einstellungen von (4). Wie groß sind die Wahrscheinlichkeiten ${\rm Pr}(z \gt 10)$ und ${\rm Pr}(z \gt 15)$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomial: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - {\rm Pr}(z \le 10) = 1 - 0.9993 = 0.0007;\hspace{0.3cm} {\rm Pr}(z \gt 15) = 0 \ {\rm (exakt)}$.
$\hspace{1.85cm}\text{Poisson: }\hspace{0.2cm} {\rm Pr}(z \gt 10) = 1 - 0.9933 = 0.0067;\hspace{0.3cm}{\rm Pr}(z \gt 15) \gt 0 \ ( \approx 0)$
$\hspace{1.85cm} \text{Näherung: }\hspace{0.2cm}{\rm Pr}(z \gt 15) \ge {\rm Pr}(z = 16) = \lambda^{16}/{16!}\approx 2 \cdot 10^{-22}$.
(6) Es gelten weiter die Einstellungen von (4). Mit welchen Parametern ergeben sich symmetrische Verteilungen um $m_1$?
$\hspace{1.0cm}\Rightarrow\hspace{0.3cm} \text{Binomialverung mit }p = 0.5\text{: }p_\mu = {\rm Pr}(z = \mu)\text{ symmetrisch um } m_1 = I/2 = 7.5 \ ⇒ \ p_μ = p_{I–μ}\ ⇒ \ p_8 = p_7, \ p_9 = p_6, \text{usw.}$
$\hspace{1.85cm}\text{Die Poissonverteilung wird dagegen nie symmetrisch, da sie sich bis ins Unendliche erstreckt!}$
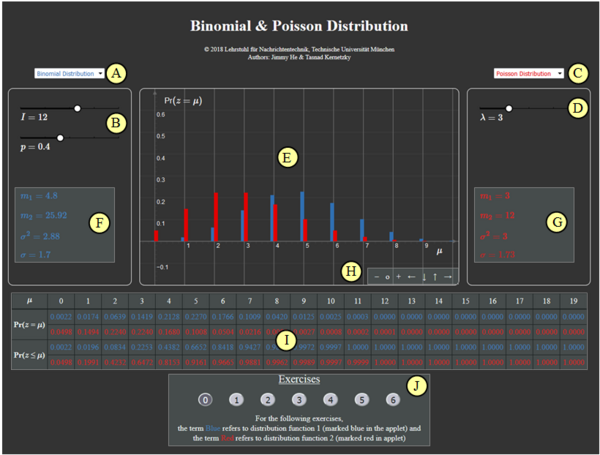
Zur Handhabung des Applets
(A) Vorauswahl für blauen Parametersatz
(B) Parametereingabe $I$ und $p$ per Slider
(C) Vorauswahl für roten Parametersatz
(D) Parametereingabe $\lambda$ per Slider
(E) Graphische Darstellung der Verteilungen
(F) Momentenausgabe für blauen Parametersatz
(G) Momentenausgabe für roten Parametersatz
(H) Variation der grafischen Darstellung
$\hspace{1.5cm}$„$+$” (Vergrößern),
$\hspace{1.5cm}$ „$-$” (Verkleinern)
$\hspace{1.5cm}$ „$\rm o$” (Zurücksetzen)
$\hspace{1.5cm}$ „$\leftarrow$” (Verschieben nach links), usw.
( I ) Ausgabe von ${\rm Pr} (z = \mu)$ und ${\rm Pr} (z \le \mu)$
(J) Bereich für die Versuchsdurchführung
Andere Möglichkeiten zur Variation der grafischen Darstellung:
- Gedrückte Shifttaste und Scrollen: Zoomen im Koordinatensystem,
- Gedrückte Shifttaste und linke Maustaste: Verschieben des Koordinatensystems.
Über die Autoren
Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.
- Die erste Version wurde 2010 von Martin Völkl im Rahmen seiner Diplomarbeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
- 2020 wurde das Programm von Veronika Hofmann (Ingenieurspraxis Mathematik, Betreuer: Benedikt Leible und Tasnád Kernetzky ) unter „HTML5” neu gestaltet.
Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster
- ↑ Shannon, C.E.: A Mathematical Theory of Communication. In: Bell Syst. Techn. J. 27 (1948), S. 379-423 und S. 623-656.