Sampling of Analog Signals and Signal Reconstruction

Inhaltsverzeichnis

1 Programmbeschreibung
2 Theoretischer Hintergrund
3 Versuchsdurchführung
4 Zur Handhabung des Applets
5 Über die Autoren
6 Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Programmbeschreibung

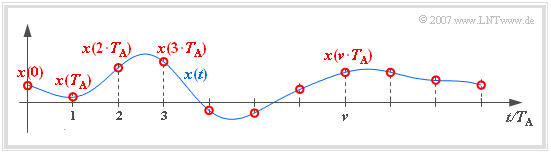
Das Applet behandelt die Systemkomponenten „Abtastung” und „Signalrekonstruktion”, zwei Komponenten, die zum Beispiel für das Verständnis der Pulscodemodulation $({\rm PCM})$ von großer Wichtigkeit sind. Die obere Grafik zeigt das für dieses Applet zugrundeliegende Modell. Darunter gezeichnet sind die Abtastwerte $x(\nu \cdot T_{\rm A})$ des zeitkontinuierlichen Signals $x(t)$. Die (unendliche) Summe über alle diese Abtastwerte bezeichnen wir als das abgetastete Signal $x_{\rm A}(t)$.

Oben: Zugrundeliegendes Modell für Abtastung und Signalrekonstruktion
Unten: Beispiel zur Zeitdiskretisierung des zeitkontinuierlichen Signals $x(t)$

Beim Sender wird aus dem zeitkontinuierlichen Quellensignal $x(t)$ das zeitdiskrete (abgetastete) Signal $x_{\rm A}(t)$ gewonnen. Man nennt diesen Vorgang Abtastung oder A/D–Wandlung.
Der entsprechende Programmparameter für den Sender ist die Abtastrate $f_{\rm A}= 1/T_{\rm A}$. In der unteren Grafik ist der Abtastabstand $T_{\rm A}$ eingezeichnet.
Beim Empfänger wird aus dem zeitdiskreten Empfangssignal $y_{\rm A}(t)$ das zeitkontinuierliche Sinkensignal $y(t)$ erzeugt ⇒ Signalrekonstruktion oder D/A–Wandlung entsprechend dem Empfänger–Frequenzgang $H_{\rm E}(f)$.

Das Applet berücksichtigt nicht die PCM–Blöcke „Quantisierung”, „Codierung / Decodierung” und der Digitale Übertragungskanal ist als ideal angenommen.

Daraus ergeben sich folgende Konsequenzen:

Im Programm ist vereinfachend $y_{\rm A}(t) = x_{\rm A}(t)$ gesetzt.
Bei geeigneten Systemparametern ist somit auch das Fehlersignal $\varepsilon(t) = y(t)-x(t)\equiv 0$ möglich.

Empfänger–Frequenzgang $H_{\rm E}(f)$

Das Abtasttheorem und die Signalrekonstruktion lassen sich im Frequenzbereich besser erklären. Im Programm werden deshalb auch alle Spektralfunktionen angezeigt;

$X(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x(t)$, $X_{\rm A}(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ x_{\rm A}(t)$, $Y(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ y(t)$, $E(f)\ \bullet\!\!-\!\!\!-\!\!\!-\!\!\circ\,\ \varepsilon(t).$

Parameter für den Empfänger–Frequenzgang $H_{\rm E}(f)$ sind die Grenzfrequenz und der Rolloff–Faktor (siehe untere Grafik):

$$f_{\rm G} = \frac{f_2 +f_1}{2},\hspace{1cm}r = \frac{f_2 -f_1}{f_2 +f_1}.$$

Hinweise:

(1) Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen.

(2) Für die ausgegebenen Leistungen gilt mit der jeweiligen Periodendauer $T_0$:

$$P_x = \frac{1}{T_0} \cdot \int_0^{T_0} x^2(t)\ {\rm d}t,\hspace{0.8cm}P_\varepsilon = \frac{1}{T_0} \cdot \int_0^{T_0} \varepsilon^2(t).$$

(3) Die Signalleistung $P_x$ und die Verzerrungsleistung $P_\varepsilon$ werden ebenfalls normiert ausgegeben, was implizit den Bezugswiderstand $R = 1\, \rm \Omega$ voraussetzt.

(4) Daraus kann der Signal–Verzerrungs–Abstand $10 \cdot \lg \ (P_x/P_\varepsilon)$ berechnet werden.

(5) Besteht die Spektralfunktion $X(f)$ bei positiven Frequenzen aus $I$ Diraclinien mit den (eventuell komplexen) Gewichten $X_1$, ... , $X_I$,
so gilt für die Sendeleistung unter Berücksichtigung der spiegelbildlichen Linien bei den negativen Frequenzen:

$$P_x = 2 \cdot \sum_{i=1}^I |X_k|^2.$$

(6) Entsprechend gilt für die Verzerrungsleistung, wenn sich die Spektralfunktion $E(f)$ im Bereich $f>0$ aus $J$ Diraclinien mit Gewichten $E_1$, ... , $E_J$ zusammensetzt:

$$P_\varepsilon = 2 \cdot \sum_{j=1}^J |E_j|^2.$$

Theoretischer Hintergrund

Beschreibung der Abtastung im Zeitbereich

Zur Zeitdiskretisierung des zeitkontinuierlichen Signals $x(t)$

Im Folgenden verwenden wir für die Beschreibung der Abtastung folgende Nomenklatur:

Das zeitkontinuierliche Signal sei $x(t)$.
Das in äquidistanten Abständen $T_{\rm A}$ abgetastete zeitdiskretisierte Signal sei $x_{\rm A}(t)$.
Außerhalb der Abtastzeitpunkte $\nu \cdot T_{\rm A}$ gilt stets $x_{\rm A}(t) \equiv 0$.
Die Laufvariable $\nu$ sei ganzzahlig: $\nu \in \mathbb{Z} = \{\hspace{0.05cm} \text{...}\hspace{0.05cm} , –3, –2, –1, \hspace{0.2cm}0, +1, +2, +3, \text{...} \hspace{0.05cm}\} $.
Dagegen ergibt sich zu den äquidistanten Abtastzeitpunkten mit der Konstanten $K$:

$$x_{\rm A}(\nu \cdot T_{\rm A}) = K \cdot x(\nu \cdot T_{\rm A})\hspace{0.05cm}.$$

Die Konstante hängt von der Art der Zeitdiskretisierung ab. Für die obige Skizze gilt $K = 1$.

Beschreibung der Abtastung mit Diracpuls

Im Folgenden gehen wir von einer geringfügig anderen Beschreibungsform aus. Die folgenden Seiten werden zeigen, dass diese gewöhnungsbedürftigen Gleichungen durchaus zu sinnvollen Ergebnissen führen, wenn man sie konsequent anwendet.

$\text{Definitionen:}$

Unter Abtastung verstehen wir hier die Multiplikation des zeitkontinuierlichen Signals $x(t)$ mit einem Diracpuls:

$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.05cm}.$$

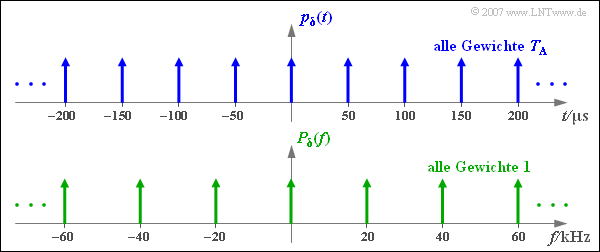
Der Diracpuls (im Zeitbereich) besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$:

$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

Aufgrund dieser Definition ergeben sich für das abgetastete Signal folgende Eigenschaften:

$$x_{\rm A}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot x(\nu \cdot T_{\rm A})\cdot \delta (t- \nu \cdot T_{\rm A} )\hspace{0.05cm}.$$

Das abgetastete Signal zum betrachteten Zeitpunkt $(\nu \cdot T_{\rm A})$ ist gleich $T_{\rm A} \cdot x(\nu \cdot T_{\rm A}) · \delta (0)$.
Da $\delta (t)$ zur Zeit $t = 0$ unendlich ist, sind eigentlich alle Signalwerte $x_{\rm A}(\nu \cdot T_{\rm A})$ ebenfalls unendlich groß und auch der oben eingeführte Faktor $K$.
Zwei Abtastwerte $x_{\rm A}(\nu_1 \cdot T_{\rm A})$ und $x_{\rm A}(\nu_2 \cdot T_{\rm A})$ unterscheiden sich jedoch im gleichen Verhältnis wie die Signalwerte $x(\nu_1 \cdot T_{\rm A})$ und $x(\nu_2 \cdot T_{\rm A})$.
Die Abtastwerte von $x(t)$ erscheinen in den Impulsgewichten der Diracfunktionen:
Die zusätzliche Multiplikation mit $T_{\rm A}$ ist erforderlich, damit $x(t)$ und $x_{\rm A}(t)$ gleiche Einheit besitzen. Beachten Sie hierbei, dass $\delta (t)$ selbst die Einheit „1/s” aufweist.

Beschreibung der Abtastung im Frequenzbereich

Zum Spektrum des abgetasteten Signals $x_{\rm A}(t)$ kommt man durch Anwendung des Faltungssatzes. Dieser besagt, dass der Multiplikation im Zeitbereich die Faltung im Spektralbereich entspricht:

$$x_{\rm A}(t) = x(t) \cdot p_{\delta}(t)\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} X_{\rm A}(f) = X(f) \star P_{\delta}(f)\hspace{0.05cm}.$$

Entwickelt man den Diracpuls $p_{\delta}(t)$ (im Zeitbereich) in eine Fourierreihe und transformiert diese unter Anwendung des Verschiebungssatzes in den Frequenzbereich, so ergibt sich mit dem Abstand $f_{\rm A} = 1/T_{\rm A}$ zweier benachbarter Diraclinien im Frequenzbereich folgende Korrespondenz ⇒ Beweis:

$$p_{\delta}(t) = \sum_{\nu = - \infty }^{+\infty} T_{\rm A} \cdot \delta(t- \nu \cdot T_{\rm A} )\hspace{0.2cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.2cm} P_{\delta}(f) = \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ).$$

Diracpuls im Zeit- und Frequenzbereich mit $T_{\rm A} = 50\ {\rm µs}$ und $f_{\rm A} = 1/T_{\rm A} = 20\ \text{kHz}$

Das Ergebnis besagt:

Der Diracpuls $p_{\delta}(t)$ im Zeitbereich besteht aus unendlich vielen Diracimpulsen, jeweils im gleichen Abstand $T_{\rm A}$ und alle mit gleichem Impulsgewicht $T_{\rm A}$.
Die Fouriertransformierte von $p_{\delta}(t)$ ergibt wiederum einen Diracpuls, aber nun im Frequenzbereich ⇒ $P_{\delta}(f)$.
Auch $P_{\delta}(f)$ besteht aus unendlich vielen Diracimpulsen, nun im jeweiligen Abstand $f_{\rm A} = 1/T_{\rm A}$ und alle mit dem Impulsgewicht $1$.
Die Abstände der Diraclinien in Zeit– und Frequenzbereich folgen demnach dem Reziprozitätsgesetz: $T_{\rm A} \cdot f_{\rm A} = 1 \hspace{0.05cm}.$

Daraus folgt: Aus dem Spektrum $X(f)$ wird durch Faltung mit der um $\mu \cdot f_{\rm A}$ verschobenen Diraclinie:

$$X(f) \star \delta (f- \mu \cdot f_{\rm A} )= X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

Wendet man dieses Ergebnis auf alle Diraclinien des Diracpulses an, so erhält man schließlich:

$$X_{\rm A}(f) = X(f) \star \sum_{\mu = - \infty }^{+\infty} \delta (f- \mu \cdot f_{\rm A} ) = \sum_{\mu = - \infty }^{+\infty} X (f- \mu \cdot f_{\rm A} )\hspace{0.05cm}.$$

$\text{Fazit:}$ Die Abtastung des analogen Zeitsignals $x(t)$ in äquidistanten Abständen $T_{\rm A}$ führt im Spektralbereich zu einer periodischen Fortsetzung von $X(f)$ mit dem Frequenzabstand $f_{\rm A} = 1/T_{\rm A}$.

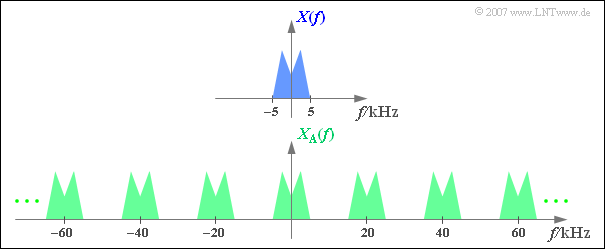
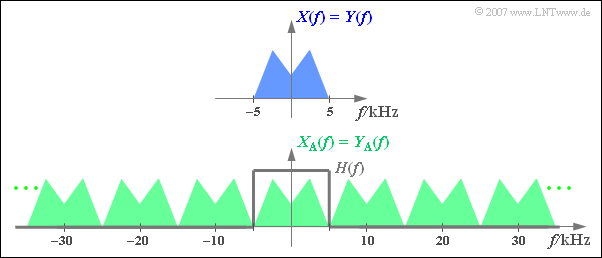
Spektrum des abgetasteten Signals

$\text{Beispiel 1:}$ Die obere Grafik zeigt (schematisch!) das Spektrum $X(f)$ eines Analogsignals $x(t)$, das Frequenzen bis $5 \text{ kHz}$ beinhaltet.

Tastet man das Signal mit der Abtastrate $f_{\rm A}\,\text{ = 20 kHz}$, also im jeweiligen Abstand $T_{\rm A}\, = {\rm 50 \, µs}$ ab, so erhält man das unten skizzierte periodische Spektrum $X_{\rm A}(f)$.

Da die Diracfunktionen unendlich schmal sind, beinhaltet das abgetastete Signal $x_{\rm A}(t)$ auch beliebig hochfrequente Anteile.
Dementsprechend ist die Spektralfunktion $X_{\rm A}(f)$ des abgetasteten Signals bis ins Unendliche ausgedehnt.

Signalrekonstruktion

Gemeinsames Modell von „Signalabtastung” und „Signalrekonstruktion”

Die Signalabtastung ist bei einem digitalen Übertragungssystem kein Selbstzweck, sondern sie muss irgendwann wieder rückgängig gemacht werden. Betrachten wir zum Beispiel das folgende System:

Das Analogsignal $x(t)$ mit der Bandbreite $B_{\rm NF}$ wird wie oben beschrieben abgetastet.
Am Ausgang eines idealen Übertragungssystems liegt das ebenfalls zeitdiskrete Signal $y_{\rm A}(t) = x_{\rm A}(t)$ vor.
Die Frage ist nun, wie der Block Signalrekonstruktion zu gestalten ist, damit auch $y(t) = x(t)$ gilt.

Frequenzbereichsdarstellung der „Signalrekonstruktion”

Die Lösung ist einfach, wenn man die Spektralfunktionen betrachtet:

Man erhält aus $Y_{\rm A}(f)$ das Spektrum $Y(f) = X(f)$ durch ein Tiefpass Filter mit dem Frequenzgang $H_{\rm E}(f)$, der

die tiefen Frequenzen unverfälscht durchlässt:

$$H_{\rm E}(f) = 1 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \le B_{\rm NF}\hspace{0.05cm},$$

die hohen Frequenzen vollständig unterdrückt:

$$H_{\rm E}(f) = 0 \hspace{0.3cm}{\rm{f\ddot{u}r}} \hspace{0.3cm} |f| \ge f_{\rm A} - B_{\rm NF}\hspace{0.05cm}.$$

Weiter ist aus der nebenstehenden Grafik zu erkennen: Solange die beiden oben genannten Bedingungen erfüllt sind, kann $H_{\rm E}(f)$ im Bereich von $B_{\rm NF}$ bis $f_{\rm A}–B_{\rm NF}$ beliebig geformt sein kann,

beispielsweise linear abfallend (gestrichelter Verlauf)
oder auch rechteckförmig,

Das Abtasttheorem

Die vollständige Rekonstruktion des Analogsignals $y(t)$ aus dem abgetasteten Signal $y_{\rm A}(t) = x_{\rm A}(t)$ ist nur möglich, wenn die Abtastrate $f_{\rm A}$ entsprechend der Bandbreite $B_{\rm NF}$ des Nachrichtensignals richtig gewählt wurde.

Aus der obigen Grafik erkennt man, dass folgende Bedingung erfüllt sein muss: $f_{\rm A} - B_{\rm NF} > B_{\rm NF} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}f_{\rm A} > 2 \cdot B_{\rm NF}\hspace{0.05cm}.$

$\text{Abtasttheorem:}$ Besitzt ein Analogsignal $x(t)$ nur Spektralanteile im Bereich $\vert f \vert < B_{\rm NF}$, so kann dieses aus seinem abgetasteten Signal $x_{\rm A}(t)$ nur dann vollständig rekonstruiert werden, wenn die Abtastrate hinreichend groß ist:

$$f_{\rm A} ≥ 2 \cdot B_{\rm NF}.$$

Für den Abstand zweier Abtastwerte muss demnach gelten:

$$T_{\rm A} \le \frac{1}{ 2 \cdot B_{\rm NF} }\hspace{0.05cm}.$$

Wird bei der Abtastung der größtmögliche Wert ⇒ $T_{\rm A} = 1/(2B_{\rm NF})$ herangezogen,

so muss zur Signalrekonstruktion des Analogsignals aus seinen Abtastwerten
ein idealer, rechteckförmiger Tiefpass mit der Grenzfrequenz $f_{\rm G} = f_{\rm A}/2 = 1/(2T_{\rm A})$ verwendet werden.

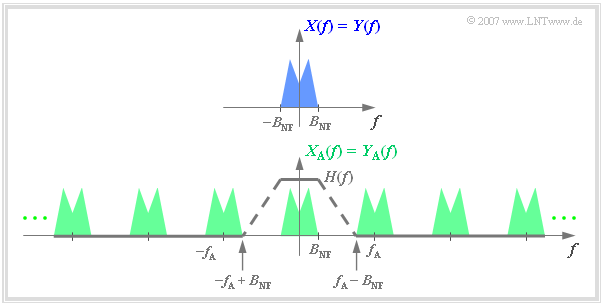
$\text{Beispiel 2:}$ Die Grafik zeigt oben das auf $\pm\text{ 5 kHz}$ begrenzte Spektrum $X(f)$ eines Analogsignals, unten das Spektrum $X_{\rm A}(f)$ des im Abstand $T_{\rm A} =\,\text{ 100 µs}$ abgetasteten Signals ⇒ $f_{\rm A}=\,\text{ 10 kHz}$.

Abtasttheorem im Frequenzbereich

Zusätzlich eingezeichnet ist der Frequenzgang $H_{\rm E}(f)$ des tiefpassartigen Empfangsfilters zur Signalrekonstruktion, dessen Grenzfrequenz exakt $f_{\rm G} = f_{\rm A}/2 = 5\,\text{ kHz}$ betragen muss.

Mit jedem anderen $f_{\rm G}$–Wert ergäbe sich $Y(f) \neq X(f)$.
Bei $f_{\rm G} < 5\,\text{ kHz}$ fehlen die oberen $X(f)$–Anteile.
Bei $f_{\rm G} > 5\,\text{ kHz}$ kommt es aufgrund von Faltungsprodukten zu unerwünschten Spektralanteilen in $Y(f)$.

Wäre am Sender die Abtastung mit einer Abtastrate $f_{\rm A} < 10\ \text{ kHz}$ erfolgt ⇒ $T_{\rm A} >100 \ {\rm µ s}$, so wäre das Analogsignal $y(t) = x(t)$ aus den Abtastwerten $y_{\rm A}(t)$ auf keinen Fall rekonstruierbar.

Versuchsdurchführung

Wählen Sie zunächst die Nummer (1, ... , 10) der zu bearbeitenden Aufgabe.
Eine Aufgabenbeschreibung wird angezeigt. Die Parameterwerte sind angepasst.
Lösung nach Drücken von „Musterlösung”.
Die Nummer 0 entspricht einem „Reset”: Gleiche Einstellung wie beim Programmstart.
Alle Signalwerte sind normiert auf $\pm 1$ zu verstehen. Auch die ausgegebenen Leistungen sind normierte Größen.

(1) Für das Quellensignal gelte $x(t) = A \cdot \cos (2\pi \cdot f_0 \cdot t -\varphi)$ mit $f_0 = \text{4 kHz}$. Abtastung mit $f_{\rm A} = \text{10 kHz}$. Rechteck–Tiefpass; Grenzfrequenz: $f_{\rm G} = \text{5 kHz}$.
Interpretieren Sie die ausgegebenen Grafiken und bewerten Sie die vorliegende Signalrekonstruktion für alle erlaubten Parameterwerte von $A$ und $\varphi$.

Das Spektrum $X(f)$ besteht aus zwei Diraclinien bei $\pm \text{4 kHz}$, jeweils mit Impulsgewicht $0.5$.
Durch die periodische Fortsetzung hat $X_{\rm A}(f)$ Linien gleicher Höhe bei $\pm \text{4 kHz}$, $\pm \text{6 kHz}$, $\pm \text{14 kHz}$, $\pm \text{16 kHz}$, $\pm \text{24 kHz}$, $\pm \text{26 kHz}$, usw.
Der Rechteck–Tiefpass mit der Grenzfrequenz $f_{\rm G} = \text{5 kHz}$ entfernt alle Linien bis auf die beiden bei $\pm \text{4 kHz}$ ⇒ $Y(f) =X(f)$ ⇒ $y(t) =x(t)$ ⇒ $P_\varepsilon = 0$.
Die Signalrekonstruktion funktioniert hier perfekt $(P_\varepsilon = 0)$ und zwar für alle Amplituden $A$ und beliebige Phasen $\varphi$.

(2) Es gelte weiter $A=1$, $f_0 = \text{4 kHz}$, $\varphi=0$, $f_{\rm A} = \text{10 kHz}$, $f_{\rm G} = \text{5 kHz}$. Welchen Einfluss haben hier die Rolloff–Faktoren $r=0.2$, $r=0.5$ und $r=1$?
Geben Sie die jeweiligen Leistungen $P_x$ und $P_\varepsilon$ an. für welche $r$–Werte ist $P_\varepsilon= 0$? Gelten diese Ergebnisse auch für andere $A$ und $\varphi$?

Die Signalleistung ist mit $|X_1|=0.5$ gleich $P_x = 2\cdot 0.5^2 = 0.5$. Die Verzerrungsleistung $P_\varepsilon$ hängt signifikant vom Rolloff–Faktor $r$ ab.
Für $r \le 0.2$ ist $P_\varepsilon=0$. Die $X_{\rm A}(f)$–Linie bei $f_0 = \text{4 kHz}$ wird durch den Tiefpass nicht verändert und die unerwünschte Linie bei $\text{6 kHz}$ voll unterdrückt.
$r = 0.5$ : $Y(f = \text{4 kHz}) = 0.35$, $Y(f = \text{6 kHz}) = 0.15$ ⇒ $|E(f = \text{4 kHz})| = |E(f = \text{6 kHz})|= 0.15$ ⇒ $P_\varepsilon = 0.09$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=7.45\ \rm dB$.
$r = 1.0$ : $Y(f = \text{4 kHz}) = 0.3$, $Y(f = \text{6 kHz}) = 0.2$ ⇒ $|E(f = \text{4 kHz})| = |E(f = \text{6 kHz})|= 0.2$ ⇒ $P_\varepsilon = 0.16$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=4.95\ \rm dB$.
Für alle $r$ ist $P_\varepsilon$ unabhängig von $\varphi$. Die Amplitude $A$ beeinflusst $P_x$ und $P_\varepsilon$ in gleicher Weise ⇒ der Quotient ist jeweils unabhängig von $A$.

(3) Nun gelte $A=1$, $f_0 = \text{5 kHz}$, $\varphi=0$, $f_{\rm A} = \text{10 kHz}$, $f_{\rm G} = \text{5 kHz}$, $r=0$ $($Rechteck–Tiefpass$)$. Interpretieren Sie das Ergebnis der Signalrekonstruktion.

$X(f)$ besteht aus zwei Diraclinien bei $\pm \text{5 kHz}$ $($Gewicht $0.5)$. Durch die periodische Fortsetzung hat $X_{\rm A}(f)$ Linien bei $\pm \text{5 kHz}$, $\pm \text{15 kHz}$, $\pm \text{25 kHz}$, usw.
Der Rechteck–Tiefpass entfernt die Linien bei $\pm \text{15 kHz}$, $\pm \text{25 kHz}$, Die Linien bei $\pm \text{5 kHz}$ werden wegen $H_{\rm E}(\pm f_{\rm G}) = H_{\rm E}(\pm \text{5 kHz}) = 0.5$ halbiert
⇒ $\text{Gewichte von }X(f = \pm \text{5 kHz})$: $0.5$ | $\text{Gewichte von }X(f_{\rm A} = \pm \text{5 kHz})$: $1.0$; | $\text{Gewichte von }Y(f = \pm \text{5 kHz})$: $0.5$ ⇒ $Y(f)=X(f)$.
Die Signalrekonstruktion funktioniert also auch hier perfekt $(P_\varepsilon = 0)$. Das gilt auch für die Phase $\varphi=180^\circ$ ⇒ $x(t) = -A \cdot \cos (2\pi \cdot f_0 \cdot t)$.

(4) Es gelten weiter die Einstellungen von (3) mit Ausnahme von $\varphi=30^\circ$. Interpretieren Sie die Unterschiede gegenüber der Einstellung (3) ⇒ $\varphi=0^\circ$.

Die Phasenbeziehung geht verloren. Das Sinkensignal $y(t)$ verläuft cosinusförmig $(\varphi_y=0^\circ)$ mit um $\cos(\varphi_x)$ kleinerer Amplitude als das Quellensignal $x(t)$.
Begründung im Frequenzbereich: Bei der periodische Fortsetzung von $X(f)$ ⇒ $X_{\rm A}(f)$ sind nur die Realteile zu addieren. Die Imaginärteile löschen sich aus.
Die $f_0$–Diraclinie von $Y(f)$ ist reell, die von $X(f)$ komplex und die von $E(f)$ imaginär ⇒ $\varepsilon(t)$ verläuft minus–sinusförmig ⇒ $P_\varepsilon = 0.125$.

Carolin: Bitte letzte Zeile der Musterlösung ändern

(5) Verdeutlichen Sie sich nochmals das Ergebnis von (4) im Vergleich zu den Einstellungen $f_0 = \text{5 kHz}$, $\varphi=30^\circ$, $f_{\rm A} = \text{11 kHz}$, $f_{\rm G} = \text{5.5 kHz}$.

Bei dieser Einstellung hat das $X_{\rm A}(f)$–Spektrum auch einen positiven Imaginärteil bei $\text{5 kHz}$ und einen negativen Imaginärteil gleicher Höhe bei $\text{6 kHz}$.
Der Rechteck–Tiefpass mit der Grenzfrequenz $\text{5.5 kHz}$ entfernt diesen zweiten Anteil. Somit ist bei dieser Einstellung $Y(f) =X(f)$ ⇒ $P_\varepsilon = 0$.
Jede $f_0$–Schwingung beliebiger Phase ist fehlerfrei aus seinen Abtastwerten rekonstruierbar, falls $f_{\rm A} = 2 \cdot f_{\rm 0} + \mu, \ f_{\rm G}= f_{\rm A}/2$ $($beliebig kleines $\mu>0)$.
Bei wertkontinuierlichem Spektrum mit $X(|f|> f_0) \equiv 0$ ⇒ $\big[$keine Diraclinien bei $\pm f_0 \big ]$ genügt grundsätzlich die Abtastrate $f_{\rm A} = 2 \cdot f_{\rm 0}$.

(6) Es gelten weiter die Einstellungen von (3) und (4) mit Ausnahme von $\varphi=90^\circ$. Interpretieren Sie die Darstellungen im Zeit– und Frequenzbereich.

Das Quellensignal wird genau bei seinen Nulldurchgängen abgetastet ⇒ $x_{\rm A}(t) \equiv 0$ ⇒ $y(t) \equiv 0$ ⇒ $\varepsilon(t)=-x(t)$ ⇒ $P_\varepsilon = P_x$ ⇒ $10 \cdot \lg \ (P_x/P_\varepsilon)=0\ \rm dB$.
Beschreibung im Frequenzbereich: Wie in (4) löschen sich die Imaginärteile von $X_{\rm A}(f)$ aus. Auch die Realteile von $X_{\rm A}(f)$ sind wegen des Sinusverlaufs Null.

(7) Nun betrachten wir das $\text {Quellensignal 2}$. Die weiteren Parameter seien $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2.5 kHz}$, $r=0$. Interpretieren Sie die Ergebnisse.

Das Quellensignal besitzt Spektralanteile bis $\pm \text{2 kHz}$. Die Signalleistung ist $P_x = 2 \cdot \big[0.1^2 + 0.25^2+0.15^2\big]= 0.19 $.
Mit der Abtastrate $f_{\rm A} = \text{5 kHz}$ sowie den Empfängerparametern $f_{\rm G} = \text{2.5 kHz}$ und $r=0$ funktioniert die Signalrekonstruktion perfekt: $P_\varepsilon = 0$.
Ebenso mit dem Trapez–Tiefpass mit $f_{\rm G} = \text{2.5 kHz}$, wenn für den Rolloff–Faktor gilt: $r \le 0.2$.

(8) Was passiert, wenn die Grenzfrequenz $f_{\rm G} = \text{1.5 kHz}$ des Rechteck–Tiefpasses zu klein ist? Interpretieren Sie insbesondere das Fehlersignal $\varepsilon(t)=y(t)-x(t)$.

Das Fehlersignal $\varepsilon(t)=-0.3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t -60^\circ)=0.3 \cdot \cos(2\pi \cdot \text{2 kHz} \cdot t +120^\circ)$ ist gleich dem (negierten) Signalanteil bei $\text{2 kHz}$. Stimmt das?
Die Verzerrungsleistung ist $P_\varepsilon(t)=2 \cdot 0.15^2= 0.045$ und der Signal–zu–Verzerrungsabstand $10 \cdot \lg \ (P_x/P_\varepsilon)=10 \cdot \lg \ (0.19/0.045)= 6.26\ \rm dB$.

(9) Was passiert, wenn die Grenzfrequenz $f_{\rm G} = \text{3.5 kHz}$ des Rechteck–Tiefpasses zu groß ist? Interpretieren Sie insbesondere das Fehlersignal $\varepsilon(t)=y(t)-x(t)$.

Das Fehlersignal $\varepsilon(t)=0.3 \cdot \cos(2\pi \cdot \text{3 kHz} \cdot t +60^\circ)$ ist nun gleich dem vom Tiefpass nicht entfernten $\text{3 kHz}$–Anteil des Sinkensignals $y(t)$. Stimmt das?
Gegenüber der Teilaufgabe (8) verändert sich die Frequenz von $\text{2 kHz}$ auf $\text{3 kHz}$ und auch die Phasenbeziehung.
Die Amplitude dieses $\text{3 kHz}$–Fehlersignals ist gleich der Amplitude des $\text{2 kHz}$–Anteils von$x(t)$. Auch hier gilt $P_\varepsilon(t)= 0.045$, $10 \cdot \lg \ (P_x/P_\varepsilon)= 6.26\ \rm dB$.

(10) Abschließend betrachten wir das $\text {Quellensignal 4}$ $($Anteile bis $\pm \text{4 kHz})$, sowie $f_{\rm A} = \text{5 kHz}$, $f_{\rm G} = \text{2.5 kHz}$, $0 \le r\le 1$. Interpretation der Ergebnisse.

Bis zum Rolloff–Faktor $r=0.2$ funktioniert die Signalrekonstruktion perfekt $(P_\varepsilon = 0)$. Erhöht man $r$, so nimmt $P_\varepsilon$ kontinuierlich zu und $10 \cdot \lg \ (P_x/P_\varepsilon)$ ab.
Mit $r=1$ werden die Signalfrequenzen $\text{0.5 kHz}$, ..., $\text{4 kHz}$ abgeschwächt, umso mehr, je höher die Frequenz ist, zum Beispiel $H_{\rm E}(f=\text{4 kHz}) = 0.6$.
Ebenso beinhaltet $Y(f)$ aufgrund der periodischen Fortsetzung auch Anteile bei den Frequenzen $\text{6 kHz}$, $\text{7 kHz}$, $\text{8 kHz}$, $\text{9 kHz}$ und $\text{9.5 kHz}$.
Zu den Abtastzeitpunkten $t\hspace{0.05cm}' = n \cdot T_{\rm A}$ stimmen $x(t\hspace{0.05cm}')$ und $y(t\hspace{0.05cm}')$ exakt überein ⇒ $\varepsilon(t\hspace{0.05cm}') = 0$. Dazwischen nicht ⇒ kleine Verzerrungsleistung $P_\varepsilon = 0.008$.

Carolin: Bitte zweite Zeile der Musterlösung ändern
Außerdem müssten bei den Signalen 2 bis 4 jeweils der Phasenwert phi_1 = 180 Grad ausgegeben werden (Realteil von 1 kHz jeweils negativ)

Zur Handhabung des Applets

(A) Auswahl: Codierung
(binär, quaternär, AMI–Code, Duobinärcode)

(B) Auswahl: Detektionsgrundimpuls
(nach Gauß–TP, CRO–Nyquist, nach Spalt–TP}

(C) Prametereingabe zu (B)
(Grenzfrequenz, Rolloff–Faktor, Rechteckdauer)

(D) Steuerung der Augendiagrammdarstellung
(Start, Pause/Weiter, Einzelschritt, Gesamt, Reset)

(E) Geschwindigkeit der Augendiagrammdarstellung

(F) Darstellung: Detektionsgrundimpuls $g_d(t)$

(G) Darstellung: Detektionsnutzsignal $d_{\rm S}(t - \nu \cdot T)$

(H) Darstellung: Augendiagramm im Bereich $\pm T$

( I ) Numerikausgabe: $ö_{\rm norm}$ (normierte Augenöffnung)

(J) Prametereingabe $10 \cdot \lg \ E_{\rm B}/N_0$ für (K)

(K) Numerikausgabe: $\sigma_{\rm norm}$ (normierter Rauscheffektivwert)

(L) Numerikausgabe: $p_{\rm U}$ (ungünstigste Fehlerwahrscheinlichkeit)

(M) Bereich für die Versuchsdurchführung: Aufgabenauswahl

(N) Bereich für die Versuchsdurchführung: Aufgabenstellung

(O) Bereich für die Versuchsdurchführung: Musterlösung einblenden

Über die Autoren

Dieses interaktive Berechnungstool wurde am Lehrstuhl für Nachrichtentechnik der Technischen Universität München konzipiert und realisiert.

Die erste Version wurde 2008 von Slim Lamine im Rahmen einer Werkstudententätigkeit mit „FlashMX–Actionscript” erstellt (Betreuer: Günter Söder).
2020 wurde das Programm von Carolin Mirschina im Rahmen einer Werkstudententätigkeit auf „HTML5” umgesetzt und neu gestaltet (Betreuer: Tasnád Kernetzky).

Die Umsetzung dieses Applets auf HTML 5 wurde durch Studienzuschüsse der Fakultät EI der TU München finanziell unterstützt. Wir bedanken uns.

Nochmalige Aufrufmöglichkeit des Applets in neuem Fenster

Applet in neuem Tab öffnen