Aufgabe 3.2: Erwartungswertberechnungen
Aus LNTwww
Wir betrachten folgende Wahrscheinlichkeitsfunktionen:
- $$P_X(X) = \big[1/2,\ 1/8,\ 0,\ 3/8 \big],$$
- $$P_Y(Y) = \big[1/2,\ 1/4,\ 1/4,\ 0 \big],$$
- $$P_U(U) = \big[1/2,\ 1/2 \big],$$
- $$P_V(V) = \big[3/4,\ 1/4\big].$$
Für die dazugehörigen Zufallsgrößen gelte:
- $X= \{0,\ 1,\ 2,\ 3\}$, $Y= \{0,\ 1,\ 2,\ 3\}$, $U = \{0,\ 1\}$, $V = \{0, 1\}$.
Oft muss man für solche diskreten Zufallsgrößen verschiedene Erwartungswerte der Form
- $${\rm E} \big [ F(X)\big ] =\hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm}\hspace{-0.03cm} {\rm supp} (P_X)} \hspace{-0.1cm} P_{X}(x) \cdot F(x) $$
berechnen. Hierbei bedeuten:
- $P_X(X)$ bezeichnet die Wahrscheinlichkeitsfunktion der diskreten Zufallsgröße $X$.
- Der "Support" von $P_X$ umfasst alle diejenigen Realisierungen $x$ der Zufallsgröße $X$ mit nicht verschwindender Wahrscheinlichkeit.
- Formal kann hierfür geschrieben werden:
- $${\rm supp} (P_X) = \{ x: \hspace{0.25cm}x \in X \hspace{0.15cm}\underline{\rm und} \hspace{0.15cm} P_X(x) \ne 0 \} \hspace{0.05cm}.$$
- $F(X)$ ist eine (beliebige) reellwertige Funktion, die im gesamten Definitionsgebiet der Zufallsgröße $X$ angebbar ist.
In der Aufgabe sollen die Erwartungswerte für verschiedene Funktionen $F(X)$ berechnet werden, unter anderem für
- $F(X)= 1/P_X(X)$,
- $F(X)= P_X(X)$,
- $F(X)= - \log_2 \ P_X(X)$.
Hinweise:
- Die Aufgabe gehört zum Kapitel Einige Vorbemerkungen zu den 2D-Zufallsgrößen.
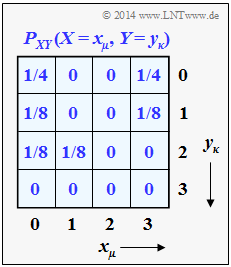
- Die beiden 1D–Wahrscheinlichkeitsfunktionen $P_X(X)$ und $P_Y(Y)$ ergeben sich aus der dargestellten 2D–PMF $P_{XY}(X,\ Y)$, wie in Aufgabe 3.2Z gezeigt werden soll.
- Zu den binären Wahrscheinlichkeitsfunktionen $P_U(U)$ und $P_V(V)$ kommt man entsprechend den Modulo–Operationen $U = X \hspace{0.1cm}\text{mod} \hspace{0.1cm}2$ sowie $V = Y \hspace{0.1cm}\text{mod} \hspace{0.1cm} 2$.
Fragebogen
Musterlösung
(1) Allgemein gilt für den Erwartungswert der Funktion $F(X)$ hinsichtlich der Zufallsvariablen $X$:
- $${\rm E} \left [ F(X)\right ] = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} {\rm supp} (P_X)} \hspace{-0.2cm} P_{X}(x) \cdot F(x) \hspace{0.05cm}.$$
Im vorliegenden Beispiel gilt dabei $X = \{0,\ 1,\ 2,\ 3\}$ und $P_X(X) = \big [1/2, \ 1/8, \ 0, \ 3/8\big ]$.
- Wegen $P_X(X = 2) = 0$ ergibt sich somit für die zu berücksichtigende Menge (dem „Support”) in obiger Summation:
- $${\rm supp} (P_X) = \{ 0\hspace{0.05cm}, 1\hspace{0.05cm}, 3 \} \hspace{0.05cm}.$$
- Mit $F(X) = 1/P_X(X)$ erhält man weiter:
- $${\rm E} \big [ 1/P_X(X)\big ] = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.4cm} P_{X}(x) \cdot {1}/{P_X(x)} = \hspace{-0.4cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} 1 \hspace{0.15cm}\underline{ = 3} \hspace{0.05cm}.$$
- Der zweite Erwartungswert liefert mit ${\rm supp} (P_Y) = \{ 0\hspace{0.05cm}, 1\hspace{0.05cm}, 2 \} $ das gleiche Ergebnis:
- $${\rm E} \left [ 1/P_Y(Y)\right ] \hspace{0.15cm}\underline{ = 3}.$$
(2) In beiden Fällen ist der Index der Wahrscheinlichkeitsfunktion mit der Zufallsvariablen $(X$ bzw. $Y)$ identisch und man erhält
- $${\rm E} \big [ P_X(X)\big ] = \hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} P_{X}(x) \cdot {P_X(x)} = (1/2)^2 + (1/8)^2 + (3/8)^2 = 13/32 \hspace{0.15cm}\underline{ \approx 0.406} \hspace{0.05cm},$$
- $${\rm E} \big [ P_Y(Y)\big ] = \hspace{-0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{-0.3cm} P_Y(y) \cdot P_Y(y) = (1/2)^2 + (1/4)^2 + (1/4)^2 \hspace{0.15cm}\underline{ = 0.375} \hspace{0.05cm}.$$
(3) Hier gelten folgende Gleichungen:
- $${\rm E} \big [ P_Y(X)\big ] = \hspace{-0.3cm} \sum_{x \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 3 \}} \hspace{-0.3cm} P_{X}(x) \cdot {P_Y(x)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{8} \cdot \frac{1}{4} + \frac{3}{8} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm},$$
- Die Erwartungswertbildung bezieht sich hier auf $P_X(·)$, also auf die Zufallsgröße $X$.
- $P_Y(·)$ ist dabei die formale Funktion ohne (direkten) Bezug zur Zufallsgröße $Y$.
- Für den zweiten Erwartungswert erhält man im vorliegenden den gleichen Zahlenwert (das muss nicht so sein):
- $${\rm E} \big [ P_X(Y)\big ] = \hspace{-0.3cm} \sum_{y \hspace{0.05cm}\in \hspace{0.05cm} \{ 0\hspace{0.05cm}, 1\hspace{0.05cm},\hspace{0.05cm} 2 \}} \hspace{-0.3cm} P_{Y}(y) \cdot {P_X(y)} = \frac{1}{2} \cdot \frac{1}{2} + \frac{1}{4} \cdot \frac{1}{8} + \frac{1}{4} \cdot 0 = 9/32 \hspace{0.15cm}\underline{ \approx 0.281} \hspace{0.05cm}.$$
(4) Wir berechnen zunächst die drei Erwartungswerte:
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_U(U)\big ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{2}{1} \hspace{0.15cm}\underline{ = 1\ {\rm bit}} \hspace{0.05cm},$$
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_V(V)\big ] = \frac{3}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{4} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 0.811\ {\rm bit}} \hspace{0.05cm},$$
- $${\rm E} \big [-{\rm log}_2 \hspace{0.1cm} P_V(U)\big ] = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{3} + \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} \frac{4}{1} \hspace{0.15cm}\underline{ = 1.208\ {\rm bit}} \hspace{0.05cm}.$$
Richtig sind demnach die beiden ersten Aussagen:
- Die Entropie $H(U) = 1$ bit kann entsprechend der ersten Gleichung berechnet werden. Sie gilt für die binäre Zufallsgröße $U$ mit gleichen Wahrscheinlichkeiten.
- Die Entropie $H(V) = 0.811$ bit berechnet sich entsprechend der zweiten Gleichung. Aufgrund der Wahrscheinlichkeiten $3/4$ und $1/4$ ist die Entropie (Unsicherheit) hier kleiner als für die Zufallsgröße $U$.
- Der dritte Erwartungswert kann schon allein vom Ergebnis her $(1.208$ bit$)$ nicht die Entropie einer binären Zufallsgröße angeben, die stets auf $1$ (bit) begrenzt ist.