Stochastische Signaltheorie/Mengentheoretische Grundlagen: Unterschied zwischen den Versionen
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 25: | Zeile 25: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die '''Vereinigungsmenge''' $C$ zweier Mengen $A$ und $B$ beinhaltet alle die Elemente, die entweder in der Menge $A$ oder der Menge $B$ oder in beiden enthalten sind (englisch: "Union Set"). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: | + | $\text{Definition:}$ Die '''Vereinigungsmenge''' (englisch: "union set") $C$ zweier Mengen $A$ und $B$ beinhaltet alle die Elemente, die entweder in der Menge $A$ oder der Menge $B$ oder in beiden enthalten sind (englisch: "Union Set"). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: |
| − | $$\ C = A \cup B | + | $$\ C = A \cup B.$$}} |
| − | |||
| − | |||
| − | |||
| − | |||
| Zeile 65: | Zeile 61: | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die '''Schnittmenge''' $C$ zweier Mengen $A$ und $B$ beinhaltet alle diejenigen Elemente, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind (englisch: ''Intersecting Set'' ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: | + | $\text{Definition:}$ Die '''Schnittmenge'''' (englisch: "intersection set") $C$ zweier Mengen $A$ und $B$ beinhaltet alle diejenigen Elemente, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind (englisch: ''Intersecting Set'' ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: |
| − | :$$C = A \cap B | + | :$$C = A \cap B .$$}} |
| − | |||
| − | |||
| Zeile 78: | Zeile 72: | ||
:$$A\cap B = B\cap A \rm \hspace{2.75cm}(Kommutativgesetz),$$ | :$$A\cap B = B\cap A \rm \hspace{2.75cm}(Kommutativgesetz),$$ | ||
:$$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(Assoziativgesetz).$$ | :$$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(Assoziativgesetz).$$ | ||
| − | + | ||
*Ist über $A$ und $B$ nichts weiter bekannt, so kann für die Wahrscheinlichkeit der Schnittmenge keine Aussage getroffen werden. | *Ist über $A$ und $B$ nichts weiter bekannt, so kann für die Wahrscheinlichkeit der Schnittmenge keine Aussage getroffen werden. | ||
*Gilt jedoch ${\rm Pr} (A) \le 1/2$ und gleichzeitig ${\rm Pr} (B) \le 1/2$, so kann eine untere und eine obere Schranke angegeben werden: | *Gilt jedoch ${\rm Pr} (A) \le 1/2$ und gleichzeitig ${\rm Pr} (B) \le 1/2$, so kann eine untere und eine obere Schranke angegeben werden: | ||
| Zeile 89: | Zeile 83: | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 2:}$ Wir betrachten | + | $\text{Beispiel 2:}$ Wir betrachten weiter das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| + | |||
| + | Wir betrachten nun die beiden Ereignisse | ||
* $A :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, und | * $A :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, und | ||
* $B :=$ „die Augenzahl ist geradzahlig”$ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$, | * $B :=$ „die Augenzahl ist geradzahlig”$ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$, | ||
| Zeile 101: | Zeile 97: | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Die '''Komplementärmenge''' (englisch: | + | $\text{Definition:}$ Die '''Komplementärmenge''' (englisch: "complementary set") von $A$ wird oft durch eine überstreichende Linie $(\overline{A})$ gekennzeichnet. Sie beinhaltet alle die Elemente, die in der Menge $A$ nicht enthalten sind, und es gilt für deren Wahrscheinlichkeit: |
:$${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$}} | :$${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$}} | ||
| Zeile 111: | Zeile 107: | ||
*Die Vereinigungsmenge einer Menge $A$ mit ihrer Komplentärmenge ergibt die Grundmenge: | *Die Vereinigungsmenge einer Menge $A$ mit ihrer Komplentärmenge ergibt die Grundmenge: | ||
:$${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$ | :$${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$ | ||
| − | *Die Schnittmenge von $A$ mit ihrer Komplementärmenge ergibt die leere Menge: | + | *Die Schnittmenge von $A$ mit ihrer Komplementärmenge ergibt die leere Menge: |
:$${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$ | :$${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$ | ||
| + | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 3:}$ Ausgehend von der Menge | + | $\text{Beispiel 3:}$ Wir betrachten weiter das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| + | |||
| + | Ausgehend von der Menge | ||
* $A :=$ „die Augenzahl ist kleiner als $5$” $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$ | * $A :=$ „die Augenzahl ist kleiner als $5$” $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$ | ||
| Zeile 126: | Zeile 125: | ||
[[Datei:P_ID19__Sto_T_1_2_S5.png | right|frame| Teilmengen im Venndiagramm]] | [[Datei:P_ID19__Sto_T_1_2_S5.png | right|frame| Teilmengen im Venndiagramm]] | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definitionen:}$ Man nennt $A$ eine '''echte Teilmenge''' von $B$ (englisch: | + | $\text{Definitionen:}$ |
| + | |||
| + | '''(1)''' Man nennt $A$ eine '''echte Teilmenge''' von $B$ (englisch: "proper subset") und schreibt hierfür $A ⊂ B$, | ||
*wenn alle Elemente von $A$ auch in $B$ enthalten sind, | *wenn alle Elemente von $A$ auch in $B$ enthalten sind, | ||
*aber nicht gleichzeitig alle Elemente von $B$ auch in $A$. | *aber nicht gleichzeitig alle Elemente von $B$ auch in $A$. | ||
| Zeile 136: | Zeile 137: | ||
Diese mengentheoretische Relation wird durch das skizzierte Venndiagramm veranschaulicht. | Diese mengentheoretische Relation wird durch das skizzierte Venndiagramm veranschaulicht. | ||
| − | + | '''(2)''' Man bezeichnet $A$ als '''unechte Teilmenge''' (englisch: "improper subset") von $B$ und verwendet die Notation | |
:$$A \subseteq B = (A \subset B) \cup (A = B),$$ | :$$A \subseteq B = (A \subset B) \cup (A = B),$$ | ||
wenn $A$ entweder eine echte Teilmenge von $B$ ist oder wenn $A$ und $B$ gleiche Mengen sind. | wenn $A$ entweder eine echte Teilmenge von $B$ ist oder wenn $A$ und $B$ gleiche Mengen sind. | ||
*Für die Wahrscheinlichkeiten gilt dann die Größenrelation ${\rm Pr} (A) \le {\rm Pr} (B)$. | *Für die Wahrscheinlichkeiten gilt dann die Größenrelation ${\rm Pr} (A) \le {\rm Pr} (B)$. | ||
| − | *Das Gleichheitszeichen gilt nur für den Sonderfall $A | + | *Das Gleichheitszeichen gilt nur für den Sonderfall $A \equiv B$.}} |
| Zeile 148: | Zeile 149: | ||
:$$(A \cup B) \cap A = A,$$ | :$$(A \cup B) \cap A = A,$$ | ||
| − | da die Schnittmenge $A ∩ B$ stets eine Teilmenge von $A$ ist, aber gleichzeitig auch $A$ eine Teilmenge der Vereinigungsmenge $A ∪ B$ | + | da die Schnittmenge $A ∩ B$ stets eine Teilmenge von $A$ ist, aber gleichzeitig auch $A$ eine Teilmenge der Vereinigungsmenge $A ∪ B$. |
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 4:}$ Wir betrachten bei unserem Standardexperiment „Werfen eines Würfels” ⇒ $G = \{1, 2, 3, 4, 5, 6\}$ nun die beiden Ereignisse | + | $\text{Beispiel 4:}$ Wir betrachten bei unserem Standardexperiment „Werfen eines Würfels” ⇒ $G = \{1, 2, 3, 4, 5, 6\}$ nun die beiden Ereignisse |
* $A :=$ „die Augenzahl ist ungerade”$ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, und | * $A :=$ „die Augenzahl ist ungerade”$ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, und | ||
* $B :=$ „die Augenzahl ist eine Primzahl” $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$. | * $B :=$ „die Augenzahl ist eine Primzahl” $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$. | ||
| Zeile 176: | Zeile 177: | ||
*Die Schnittmenge $A ∩ B$ (im Bild violett dargestellt) ist weder horizontal noch vertikal schraffiert. | *Die Schnittmenge $A ∩ B$ (im Bild violett dargestellt) ist weder horizontal noch vertikal schraffiert. | ||
| − | *Das Komplement $\overline{A ∩ B}$ der Schnittmenge ist dementsprechend entweder horizontal, vertikal oder in beiden Richtungen schraffiert. | + | *Das Komplement $\overline{A ∩ B}$ der Schnittmenge ist dementsprechend entweder horizontal, vertikal oder in beiden Richtungen schraffiert. |
*Nach dem zweiten Theorem von de Morgan ist das Komplement der Schnittmenge gleich der Vereinigungsmenge der beiden Komplentärmengen von $A$ und $B$: | *Nach dem zweiten Theorem von de Morgan ist das Komplement der Schnittmenge gleich der Vereinigungsmenge der beiden Komplentärmengen von $A$ und $B$: | ||
:$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$ | :$$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$ | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 5:}$ Wir betrachten die beiden Mengen | + | $\text{Beispiel 5:}$ Wir betrachten wieder das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| + | |||
| + | Wir betrachten nun die beiden Mengen | ||
* $A : =$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$, | * $A : =$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$, | ||
* $B : =$ „die Augenzahl ist größer als $2$” $= \{3, 4, 5, 6\}$. | * $B : =$ „die Augenzahl ist größer als $2$” $= \{3, 4, 5, 6\}$. | ||
| Zeile 192: | Zeile 195: | ||
Weiter erhält man mit den obigen Theoremen die folgenden Teilmengen: | Weiter erhält man mit den obigen Theoremen die folgenden Teilmengen: | ||
| − | :$$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\} | + | :$$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\},$$ |
| + | :$$\overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$}} | ||
==Disjunkte Mengen== | ==Disjunkte Mengen== | ||
<br> | <br> | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Zwei Mengen $A$ und $B$ nennt man '''disjunkt''' (englisch: | + | $\text{Definition:}$ Zwei Mengen $A$ und $B$ nennt man '''disjunkt''' (englisch: "disjoint") oder '''miteinander unvereinbar''', |
*wenn es kein einziges Element gibt, | *wenn es kein einziges Element gibt, | ||
*das sowohl in $A$ als auch in $B$ enthalten ist.}} | *das sowohl in $A$ als auch in $B$ enthalten ist.}} | ||
| Zeile 223: | Zeile 227: | ||
==Additionstheorem== | ==Additionstheorem== | ||
<br> | <br> | ||
| − | Nur bei disjunkten Mengen $A$ und $B$ gilt für die Wahrscheinlichkeit der Vereinigungsmenge der Zusammenhang ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$. Wie errechnet sich diese Wahrscheinlichkeit aber bei allgemeinen, nicht notwendigerweise disjunkten Ereignissen? | + | Nur bei disjunkten Mengen $A$ und $B$ gilt für die Wahrscheinlichkeit der Vereinigungsmenge der Zusammenhang ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$. |
| + | |||
| + | Wie errechnet sich diese Wahrscheinlichkeit aber bei allgemeinen, nicht notwendigerweise disjunkten Ereignissen? | ||
[[Datei:P_ID21__Sto_T_1_2_S8.png | right|frame| Zum Additionstheorem der Wahrscheinlichkeitsrechnung]] | [[Datei:P_ID21__Sto_T_1_2_S8.png | right|frame| Zum Additionstheorem der Wahrscheinlichkeitsrechnung]] | ||
Betrachten Sie das rechte Venndiagramm mit der violett dargestellten Schnittmenge $A ∩ B$. | Betrachten Sie das rechte Venndiagramm mit der violett dargestellten Schnittmenge $A ∩ B$. | ||
| − | *Die rote Menge beinhaltet alle Elemente, die zu $A$ gehören, aber nicht zu $B$. | + | *Die rote Menge beinhaltet alle Elemente, die zu $A$ gehören, aber nicht zu $B$. |
| − | *Die Elemente von $B$, die nicht gleichzeitig in $A$ enthalten sind, sind blau dargestellt. | + | *Die Elemente von $B$, die nicht gleichzeitig in $A$ enthalten sind, sind blau dargestellt. |
| − | *Alle roten, blauen und violetten Flächen zusammen ergeben die Vereinigungsmenge $A ∪ B$. | + | *Alle roten, blauen und violetten Flächen zusammen ergeben die Vereinigungsmenge $A ∪ B$. |
| Zeile 235: | Zeile 241: | ||
:$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ | :$${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$ | ||
:$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ | :$${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$ | ||
| − | :$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) | + | :$${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) + {\rm Pr}(\overline{A} \cap {B}).$$ |
| − | Addiert man die ersten beiden Gleichungen und subtrahiert davon die dritte, so erhält man: | + | Addiert man die ersten beiden Gleichungen und subtrahiert davon die dritte, so erhält man: |
| − | :$${\rm Pr}(A) | + | :$${\rm Pr}(A) +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$ |
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| − | $\text{Definition:}$ Durch Umstellen dieser Gleichung kommt man zum sogenannten '''Additionstheorem''' (englisch: | + | $\text{Definition:}$ Durch Umstellen dieser Gleichung kommt man zum sogenannten '''Additionstheorem''' (englisch: "Addition Rule") für zwei beliebige, nicht notwendigerweise disjunkte Ereignisse: |
:$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$}} | :$${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$}} | ||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 7:}$ Wir betrachten die beiden Mengen | + | $\text{Beispiel 7:}$ Wir beziehen uns wieder auf das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$. |
| − | * $A :=$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und | + | |
| + | Wir betrachten die beiden Mengen | ||
| + | * $A :=$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und | ||
* $B :=$ „die Augenzahl ist größer als $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$. | * $B :=$ „die Augenzahl ist größer als $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$. | ||
Damit ergeben sich für die Wahrscheinlichkeiten | Damit ergeben sich für die Wahrscheinlichkeiten | ||
| − | *der Vereinigungsmenge ⇒ ${\rm Pr}(A ∪ B) = 5/6$, und | + | *der Vereinigungsmenge ⇒ ${\rm Pr}(A ∪ B) = 5/6$, und |
*der Schnittmenge ⇒ ${\rm Pr}(A ∩ B) = 2/6$. | *der Schnittmenge ⇒ ${\rm Pr}(A ∩ B) = 2/6$. | ||
| Zeile 260: | Zeile 268: | ||
==Vollständiges System== | ==Vollständiges System== | ||
<br> | <br> | ||
| − | Im letzten Abschnitt zu diesem Kapitel betrachten wir wieder mehr als zwei mögliche Ereignisse, nämlich allgemein $I$. Diese Ereignisse werden im Folgenden mit $A_i$ bezeichnet, und es gilt für den Laufindex: $1 ≤ i ≤ I$. | + | Im letzten Abschnitt zu diesem Kapitel betrachten wir wieder mehr als zwei mögliche Ereignisse, nämlich allgemein $I$. |
| + | |||
| + | Diese Ereignisse werden im Folgenden mit $A_i$ bezeichnet, und es gilt für den Laufindex: $1 ≤ i ≤ I$. | ||
{{BlaueBox|TEXT= | {{BlaueBox|TEXT= | ||
| Zeile 268: | Zeile 278: | ||
:$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$ | :$$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$ | ||
'''(2)''' Die Vereinigung aller Ereignismengen ergibt die Grundmenge: | '''(2)''' Die Vereinigung aller Ereignismengen ergibt die Grundmenge: | ||
| − | :$$\bigcup_{i=1}^{I} A_i = G.$$ | + | :$$\bigcup_{i=1}^{I} A_i = G.$$ |
| + | Aufgrund dieser beiden Voraussetzungen gilt dann für die Summe aller Wahrscheinlichkeiten: | ||
| + | :$$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$}} | ||
| − | |||
| − | |||
{{GraueBox|TEXT= | {{GraueBox|TEXT= | ||
| − | $\text{Beispiel 8:}$ Die Ereignismengen $A_1 := \{1, 5\}$ und $A_2 := \{2, 3\}$ ergeben beim Zufallsexperiment „Werfen eines Würfels” zusammen mit der Menge $A_3 := \{4, 6\}$ ein vollständiges System, nicht jedoch beim Experiment „Werfen einer Roulettekugel”.}} | + | $\text{Beispiel 8:}$ Die Ereignismengen $A_1 := \{1, 5\}$ und $A_2 := \{2, 3\}$ ergeben |
| + | *beim Zufallsexperiment „Werfen eines Würfels” zusammen mit der Menge $A_3 := \{4, 6\}$ ein vollständiges System, | ||
| + | *nicht jedoch beim Experiment „Werfen einer Roulettekugel”.}} | ||
| Zeile 296: | Zeile 308: | ||
''Hinweise:'' | ''Hinweise:'' | ||
| − | *Die [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Wahrscheinlichkeitsfunktion_und_Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsfunktion]] $P_X(X)$ macht nur Aussagen über die Wahrscheinlichkeiten, nicht über den Wertevorrat $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ der Zufallsgröße $X$. | + | *Die [[Informationstheorie/Einige_Vorbemerkungen_zu_zweidimensionalen_Zufallsgrößen#Wahrscheinlichkeitsfunktion_und_Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsfunktion]] $($englisch: "probability mass function", $\rm PMF)$ $P_X(X)$ macht nur Aussagen über die Wahrscheinlichkeiten, nicht über den Wertevorrat $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ der Zufallsgröße $X$. |
| − | *Diese zusätzliche Information liefert die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion_(WDF)#Definition_der_Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion]] (WDF).}} | + | *Diese zusätzliche Information liefert die [[Stochastische_Signaltheorie/Wahrscheinlichkeitsdichtefunktion_(WDF)#Definition_der_Wahrscheinlichkeitsdichtefunktion|Wahrscheinlichkeitsdichtefunktion]] $\rm (WDF)$; englische Bezeichnung: "probability density function" $\rm (PDF)$.}} |
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| Zeile 305: | Zeile 317: | ||
[[Aufgaben:1.2Z_Ziffernmengen|Aufgabe 1.2Z: Ziffernmengen]] | [[Aufgaben:1.2Z_Ziffernmengen|Aufgabe 1.2Z: Ziffernmengen]] | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_1.3:_Fiktive_Uni_Irgendwo|Aufgabe 1.3: Fiktive Uni Irgendwo]] |
[[Aufgaben:Aufgabe_1.3Z:_Gewinnen_mit_Roulette%3F|Aufgabe 1.3Z: Gewinnen mit Roulette?]] | [[Aufgaben:Aufgabe_1.3Z:_Gewinnen_mit_Roulette%3F|Aufgabe 1.3Z: Gewinnen mit Roulette?]] | ||
Aktuelle Version vom 18. November 2021, 14:09 Uhr
Inhaltsverzeichnis
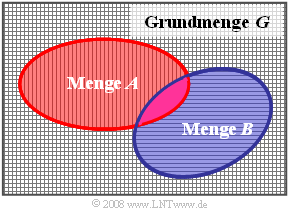
Venndiagramm, Grundmenge und leere Menge
In späteren Kapitel wird manchmal auf die Mengenlehre Bezug genommen. Deshalb sollen hier die wichtigsten Grundlagen und Definitionen dieser Disziplin kurz zusammengefasst werden. Die Thematik wird auch im Lernvideo Mengentheoretische Begriffe und Gesetzmäßigkeiten am Beispiel europäischer Staaten behandelt.
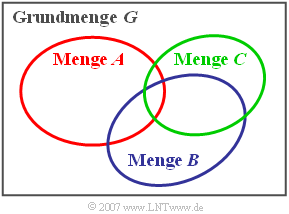
Ein wichtiges Hilfsmittel der Mengenlehre ist das Venndiagramm gemäß der Grafik:
- Angewandt auf die Wahrscheinlichkeitsrechnung sind hier die Ereignisse $A_i$ als Flächenbereiche dargestellt. Zur einfacheren Beschreibung bezeichnen wir hier die Ereignisse im Gegensatz zum letzten Kapitel nicht mit $A_1$, $A_2$ und $A_3$, sondern mit $A$, $B$ und $C$. Die Gesamtfläche entspricht der Grundmenge $G$.
- Die Grundmenge $G$ beinhaltet alle möglichen Ergebnisse und steht für das Sichere Ereignis, das definitionsgemäß mit der Wahrscheinlichkeit „Eins” eintritt: ${\rm Pr}(G) = 1$. Zum Beispiel ist beim Zufallsexperiment „Werfen eines Würfels” die Wahrscheinlichkeit für das Ereignis „die Augenzahl ist kleiner oder gleich 6” identisch Eins.
- Dagegen beinhaltet die Leere Menge $ϕ$ kein einziges Element. Bezogen auf Ereignisse gibt die Leere Menge das Unmögliche Ereignis mit der Wahrscheinlichkeit ${\rm Pr}(ϕ) = 0$ an. Beispielsweise ist beim Experiment „Werfen eines Würfels”' die Wahrscheinlichkeit für das Ereignis „die Augenzahl ist größer als 6” identisch Null.
Anzumerken ist, dass nicht jedes Ereignis $A$ mit ${\rm Pr}(A) = 0$ wirklich nie eintreten kann:
- So ist die Wahrscheinlichkeit des Ereignisses „der Rauschwert $n$ ist identisch Null” zwar verschwindend klein und es gilt ${\rm Pr}(n \equiv 0) = 0$, wenn $n$ durch eine kontinuierliche (Gaußsche) Zufallsgröße beschrieben wird.
- Trotzdem ist es natürlich möglich (wenn auch extrem unwahrscheinlich), dass irgendwann auch der exakte Rauschwert $n = 0$ auftritt.
Vereinigungsmenge
Anhand des Venndiagramms werden nun einige mengentheoretische Verknüpfungen erläutert.
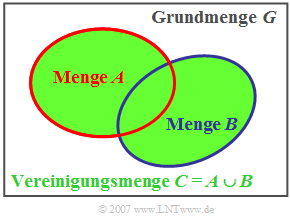
$\text{Definition:}$ Die Vereinigungsmenge (englisch: "union set") $C$ zweier Mengen $A$ und $B$ beinhaltet alle die Elemente, die entweder in der Menge $A$ oder der Menge $B$ oder in beiden enthalten sind (englisch: "Union Set"). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt: $$\ C = A \cup B.$$
Anhand der Grafik sind die folgenden Gesetzmäßigkeiten der Mengenlehre leicht einzusehen:
- $$A \cup \it \phi = A \rm \hspace{3.6cm}(Vereinigung \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}leeren \hspace{0.15cm}Menge),$$
- $$A\cup G = G \rm \hspace{3.6cm}(Vereinigung \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}Grundmenge),$$
- $$A\cup A = A \hspace{3.6cm}(\rm Tautologiegesetz),$$
- $$A\cup B = B\cup A \hspace{2.75cm}(\rm Kommutativgesetz),$$
- $$(A\cup B)\cup C = A\cup (B\cup C) \hspace{0.45cm}(\rm Assoziativgesetz).$$
Ist über die Ereignismengen $A$ und $B$ nichts weiter bekannt, so können für die Wahrscheinlichkeit der Vereinigungsmenge nur eine untere und eine obere Schranke angegeben werden:
- $${\rm Max}\big({\rm Pr} (A), \ {\rm Pr} (B)\big) \le {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B).$$
- Die Wahrscheinlichkeit der Vereinigungsmenge ist gleich der unteren Schranke, wenn $A$ eine Teilmenge von $B$ ist oder umgekehrt.
- Die obere Schranke gilt für disjunkte Mengen.
$\text{Beispiel 1:}$ Wir betrachten wieder das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Betrachtet man die beiden Ereignisse
- $A :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$,
- $B :=$ „die Augenzahl ist geradzahlig” $= \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
so beinhaltet die Vereinigungsmenge vier Elemente: $(A \cup B) = \{2, 4, 5, 6 \}$ ⇒ ${\rm Pr} (A \cup B) = 4/6 = 2/3$.
- Die untere Schranke ergibt sich zu ${\rm Pr} (A \cup B) \ge {\rm Max}\big({\rm Pr} (A),\ {\rm Pr} (B)\big ) = 3/6.$
- Für die obere Schranke gilt $ {\rm Pr} (A \cup B) \le {\rm Pr} (A)+{\rm Pr} (B) = 5/6.$
Schnittmenge
Eine weitere wichtige mengentheoretische Verknüpfung stellt die Schnittmenge dar.
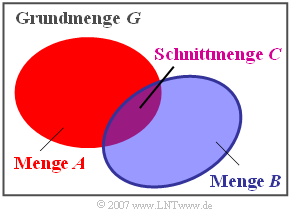
$\text{Definition:}$ Die Schnittmenge' (englisch: "intersection set") $C$ zweier Mengen $A$ und $B$ beinhaltet alle diejenigen Elemente, die sowohl in der Menge $A$ als auch in der Menge $B$ enthalten sind (englisch: Intersecting Set ). Formelmäßig wird dieser Zusammenhang wie folgt ausgedrückt:
- $$C = A \cap B .$$
In der Grafik ist die Schnittmenge violett dargestellt. Analog zur Vereinigungsmenge sind hier folgende Gesetzmäßigkeiten zu nennen:
- $$A \cap \it \phi = \it \phi \rm \hspace{3.75cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}leeren \hspace{0.15cm}Menge),$$
- $$A \cap G = A \rm \hspace{3.6cm}(Schnitt \hspace{0.15cm}mit \hspace{0.15cm}der \hspace{0.15cm}Grundmenge),$$
- $$A\cap A = A \rm \hspace{3.6cm}(Tautologiegesetz),$$
- $$A\cap B = B\cap A \rm \hspace{2.75cm}(Kommutativgesetz),$$
- $$(A\cap B)\cap C = A\cap (B\cap C) \rm \hspace{0.45cm}(Assoziativgesetz).$$
- Ist über $A$ und $B$ nichts weiter bekannt, so kann für die Wahrscheinlichkeit der Schnittmenge keine Aussage getroffen werden.
- Gilt jedoch ${\rm Pr} (A) \le 1/2$ und gleichzeitig ${\rm Pr} (B) \le 1/2$, so kann eine untere und eine obere Schranke angegeben werden:
- $$0 \le {\rm Pr} (A ∩ B) \le {\rm Min}\ \big({\rm Pr} (A),\ {\rm Pr} (B)\big ).$$
- ${\rm Pr}(A ∩ B)$ wird manchmal auch „Verbundwahrscheinlichkeit” genannt und mit ${\rm Pr}(A, \ B)$ bezeichnet.
- ${\rm Pr}(A ∩ B)$ ist gleich der oberen Schranke, wenn $A$ eine Teilmenge von $B$ ist oder umgekehrt.
- Die untere Schranke ergibt sich für die Verbundwahrscheinlichkeit von disjunkten Mengen.
$\text{Beispiel 2:}$ Wir betrachten weiter das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Wir betrachten nun die beiden Ereignisse
- $A :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (A)= 2/6= 1/3$, und
- $B :=$ „die Augenzahl ist geradzahlig”$ = \{2, 4, 6\}$ ⇒ ${\rm Pr} (B)= 3/6= 1/2$,
Die Schnittmenge beinhaltet nur ein einziges Element: $(A ∩ B) = \{ 6 \}$ ⇒ ${\rm Pr} (A ∩ B) = 1/6$.
- Die obere Schranke ergibt sich zu ${\rm Pr} (A ∩ B) \le {\rm Min}\ \big ({\rm Pr} (A), \, {\rm Pr} (B)\big ) = 2/6.$
- Die untere Schranke der Schnittmenge ist hier wegen ${\rm Pr} (A) \le 1/2$ und ${\rm Pr} (B) \le 1/2$ gleich Null.
Komplementärmenge
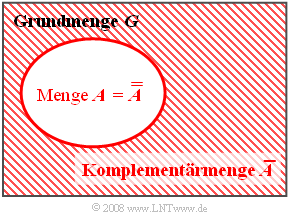
$\text{Definition:}$ Die Komplementärmenge (englisch: "complementary set") von $A$ wird oft durch eine überstreichende Linie $(\overline{A})$ gekennzeichnet. Sie beinhaltet alle die Elemente, die in der Menge $A$ nicht enthalten sind, und es gilt für deren Wahrscheinlichkeit:
- $${\rm Pr}(\overline{A}) = 1- {\rm Pr}(A).$$
Im dargestellten Venndiagramm ist die zu $A$ komplementäre Menge schraffiert dargestellt. Aus diesem Schaubild sind einige mengentheoretische Beziehungen zu erkennen:
- Die Komplementärmenge der komplementären Menge von $A$ ist die Menge $A$ selbst:
- $$\overline{\overline{A}} = A.$$
- Die Vereinigungsmenge einer Menge $A$ mit ihrer Komplentärmenge ergibt die Grundmenge:
- $${\rm Pr}(A \cup \overline{A}) = {\rm Pr}(G) = \rm 1.$$
- Die Schnittmenge von $A$ mit ihrer Komplementärmenge ergibt die leere Menge:
- $${\rm Pr}(A \cap \overline{A}) = {\rm Pr}({\it \phi}) \rm = 0.$$
$\text{Beispiel 3:}$ Wir betrachten weiter das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Ausgehend von der Menge
- $A :=$ „die Augenzahl ist kleiner als $5$” $= \{1, 2, 3, 4\}$ ⇒ ${\rm Pr} (A)= 2/3$
lautet die zugehörige Komplentärmenge:
- $\overline{A} :=$ „die Augenzahl ist größer oder gleich $5$”$ = \{5, 6\}$ ⇒ ${\rm Pr} (\overline{A})= 1 - {\rm Pr} (A) = 1 - 2/3 = 1/3.$
Echte Teilmenge – Unechte Teilmenge
$\text{Definitionen:}$
(1) Man nennt $A$ eine echte Teilmenge von $B$ (englisch: "proper subset") und schreibt hierfür $A ⊂ B$,
- wenn alle Elemente von $A$ auch in $B$ enthalten sind,
- aber nicht gleichzeitig alle Elemente von $B$ auch in $A$.
In diesem Fall gilt für die Wahrscheinlichkeiten:
- $${\rm Pr}(A) < {\rm Pr}(B).$$
Diese mengentheoretische Relation wird durch das skizzierte Venndiagramm veranschaulicht.
(2) Man bezeichnet $A$ als unechte Teilmenge (englisch: "improper subset") von $B$ und verwendet die Notation
- $$A \subseteq B = (A \subset B) \cup (A = B),$$
wenn $A$ entweder eine echte Teilmenge von $B$ ist oder wenn $A$ und $B$ gleiche Mengen sind.
- Für die Wahrscheinlichkeiten gilt dann die Größenrelation ${\rm Pr} (A) \le {\rm Pr} (B)$.
- Das Gleichheitszeichen gilt nur für den Sonderfall $A \equiv B$.
Daneben gelten aber auch die beiden als Absorptionsgesetze bekannten Gleichungen:
- $$(A \cap B) \cup A = A ,$$
- $$(A \cup B) \cap A = A,$$
da die Schnittmenge $A ∩ B$ stets eine Teilmenge von $A$ ist, aber gleichzeitig auch $A$ eine Teilmenge der Vereinigungsmenge $A ∪ B$.
$\text{Beispiel 4:}$ Wir betrachten bei unserem Standardexperiment „Werfen eines Würfels” ⇒ $G = \{1, 2, 3, 4, 5, 6\}$ nun die beiden Ereignisse
- $A :=$ „die Augenzahl ist ungerade”$ = \{1, 3, 5\}$ ⇒ ${\rm Pr} (A)= 3/6$, und
- $B :=$ „die Augenzahl ist eine Primzahl” $= \{1, 2, 3, 5\}$ ⇒ ${\rm Pr} (B)= 4/6$.
Man erkennt, dass $A$ eine (echte) Teilmenge der Menge $B$ ist. Dementsprechend gilt auch ${\rm Pr} (A) < {\rm Pr} (B).$
Theoreme von de Morgan
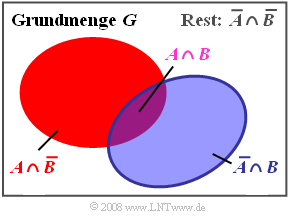
Bei vielen Aufgaben aus der Mengenlehre sind die beiden Theoreme von de Morgan äußerst nützlich. Diese lauten:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B},$$
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
Diese Gesetzmäßigkeiten sind im Schaubild veranschaulicht:
- Die Menge $A$ ist rot dargestellt und die Menge $B$ blau.
- Die Komplentärmenge $\overline {A}$ von $A$ ist in horizontaler Richtung schraffiert.
- Die Komplentärmenge $\overline {B}$ von $B$ ist in vertikaler Richtung schraffiert.
- Das Komplement $\overline{A \cup B}$ der Vereinigungsmenge ${A \cup B}$ ist sowohl horizontal als auch vertikal schraffiert.
- Es ist damit gleich der Schnittmenge $\overline{A} \cap \overline{B}$ der beiden Komplentärmengen von $A$ und $B$:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B}.$$
Auch die zweite Form des de Morgan-Theorems lässt sich mit diesem Venndiagramm grafisch verdeutlichen:
- Die Schnittmenge $A ∩ B$ (im Bild violett dargestellt) ist weder horizontal noch vertikal schraffiert.
- Das Komplement $\overline{A ∩ B}$ der Schnittmenge ist dementsprechend entweder horizontal, vertikal oder in beiden Richtungen schraffiert.
- Nach dem zweiten Theorem von de Morgan ist das Komplement der Schnittmenge gleich der Vereinigungsmenge der beiden Komplentärmengen von $A$ und $B$:
- $$\overline{A \cap B} = \overline{A} \cup \overline{B}.$$
$\text{Beispiel 5:}$ Wir betrachten wieder das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Wir betrachten nun die beiden Mengen
- $A : =$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$,
- $B : =$ „die Augenzahl ist größer als $2$” $= \{3, 4, 5, 6\}$.
Daraus folgen die beiden komplementären Mengen
- $\overline {A} : =$ „die Augenzahl ist geradzahlig” $= \{2, 4, 6\}$,
- $\overline {B} : =$ „die Augenzahl ist kleiner als $3$” $= \{1, 2\}$.
Weiter erhält man mit den obigen Theoremen die folgenden Teilmengen:
- $$\overline{A \cup B} = \overline{A} \cap \overline{B} = \{2\},$$
- $$\overline{\it A \cap \it B} =\overline{\it A} \cup \overline{\it B} = \{1,2,4,6\}.$$
Disjunkte Mengen
$\text{Definition:}$ Zwei Mengen $A$ und $B$ nennt man disjunkt (englisch: "disjoint") oder miteinander unvereinbar,
- wenn es kein einziges Element gibt,
- das sowohl in $A$ als auch in $B$ enthalten ist.
Das Schaubild zeigt zwei disjunkte Mengen $A$ und $B$ im Venndiagramm.
In diesem Sonderfall gelten die folgenden Aussagen:
- Die Schnittmenge zweier disjunkter Mengen $A$ und $B$ ergibt stets die leere Menge:
- $${\rm Pr}(A \cap B) = {\rm Pr}(\phi) = \rm 0.$$
- Die Wahrscheinlichkeit der Vereinigungsmenge zweier disjunkter Mengen $A$ und $B$ ist immer gleich der Summe der beiden Einzelwahrscheinlichkeiten:
- $${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B).$$
$\text{Beispiel 6:}$ Bei unserem Standardexperiment sind die beiden Mengen
- $A :=$ „die Augenzahl ist kleiner als $3$”$ = \{1, 2\}$ ⇒ ${\rm Pr}( A) = 2/6$, und
- $B :=$ „die Augenzahl ist größer als $3$” $ = \{4, 5,6\}$ ⇒ ${\rm Pr}( B) = 3/6$
zueinander disjunkt, da $A$ und $B$ kein einziges gemeinsames Element beinhalten.
- Die Schnittmenge ergibt die leere Menge: ${A \cap B} = \phi$.
- Die Wahrscheinlichkeit der Vereinigungsmenge ${A \cup B} = \{1, 2, 4, 5, 6\}$ ist gleich ${\rm Pr}( A) + {\rm Pr}(B) = 5/6.$
Additionstheorem
Nur bei disjunkten Mengen $A$ und $B$ gilt für die Wahrscheinlichkeit der Vereinigungsmenge der Zusammenhang ${\rm Pr}( A \cup B) = {\rm Pr}( A) + {\rm Pr}(B)$.
Wie errechnet sich diese Wahrscheinlichkeit aber bei allgemeinen, nicht notwendigerweise disjunkten Ereignissen?
Betrachten Sie das rechte Venndiagramm mit der violett dargestellten Schnittmenge $A ∩ B$.
- Die rote Menge beinhaltet alle Elemente, die zu $A$ gehören, aber nicht zu $B$.
- Die Elemente von $B$, die nicht gleichzeitig in $A$ enthalten sind, sind blau dargestellt.
- Alle roten, blauen und violetten Flächen zusammen ergeben die Vereinigungsmenge $A ∪ B$.
Aus dieser mengentheoretischen Darstellung erkennt man folgende Zusammenhänge:
- $${\rm Pr}(A) \hspace{0.8cm}= {\rm Pr}(A \cap B) + {\rm Pr}(A \cap \overline{B}),$$
- $${\rm Pr}(B) \hspace{0.8cm}= {\rm Pr}(A \cap B) \rm +{\rm Pr}(\overline{A} \cap {B}),$$
- $${\rm Pr}(A \cup B) ={\rm Pr}(A \cap B) +{\rm Pr} ({A} \cap \overline{B}) + {\rm Pr}(\overline{A} \cap {B}).$$
Addiert man die ersten beiden Gleichungen und subtrahiert davon die dritte, so erhält man:
- $${\rm Pr}(A) +{\rm Pr}(B) -{\rm Pr}(A \cup B) = {\rm Pr}(A \cap B).$$
$\text{Definition:}$ Durch Umstellen dieser Gleichung kommt man zum sogenannten Additionstheorem (englisch: "Addition Rule") für zwei beliebige, nicht notwendigerweise disjunkte Ereignisse:
- $${\rm Pr}(A \cup B) = {\rm Pr}(A) + {\rm Pr}(B) - {\rm Pr}(A \cap B).$$
$\text{Beispiel 7:}$ Wir beziehen uns wieder auf das Experiment „Werfen eines Würfels”. Die möglichen Ergebnisse sind somit $E_μ ∈ G = \{1, 2, 3, 4, 5, 6\}$.
Wir betrachten die beiden Mengen
- $A :=$ „die Augenzahl ist ungeradzahlig” $= \{1, 3, 5\}$ ⇒ ${\rm Pr}(A) = 3/6$, und
- $B :=$ „die Augenzahl ist größer als $2$”$ = \{3, 4, 5, 6\}$ ⇒ ${\rm Pr}(B) = 4/6$.
Damit ergeben sich für die Wahrscheinlichkeiten
- der Vereinigungsmenge ⇒ ${\rm Pr}(A ∪ B) = 5/6$, und
- der Schnittmenge ⇒ ${\rm Pr}(A ∩ B) = 2/6$.
Die Zahlenwerte zeigen die Gültigkeit des Additionstheorems: $5/6 = 3/6 + 4/6 − 2/6$.
Vollständiges System
Im letzten Abschnitt zu diesem Kapitel betrachten wir wieder mehr als zwei mögliche Ereignisse, nämlich allgemein $I$.
Diese Ereignisse werden im Folgenden mit $A_i$ bezeichnet, und es gilt für den Laufindex: $1 ≤ i ≤ I$.
$\text{Definition:}$ Eine Konstellation mit den Ereignissen $A_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_i, \hspace{0.1cm}\text{...}\hspace{0.1cm} , A_I$ bezeichnet man dann und nur dann als ein vollständiges System, wenn die beiden folgenden Bedingungen erfüllt sind:
(1) Alle Ereignisse sind paarweise disjunkt:
- $$A_i \cap A_j = \it \phi \hspace{0.15cm}\rm f\ddot{u}r\hspace{0.15cm}alle\hspace{0.15cm}\it i \ne j.$$
(2) Die Vereinigung aller Ereignismengen ergibt die Grundmenge:
- $$\bigcup_{i=1}^{I} A_i = G.$$
Aufgrund dieser beiden Voraussetzungen gilt dann für die Summe aller Wahrscheinlichkeiten:
- $$\sum_{i =1}^{ I} {\rm Pr}(A_i) = 1.$$
$\text{Beispiel 8:}$ Die Ereignismengen $A_1 := \{1, 5\}$ und $A_2 := \{2, 3\}$ ergeben
- beim Zufallsexperiment „Werfen eines Würfels” zusammen mit der Menge $A_3 := \{4, 6\}$ ein vollständiges System,
- nicht jedoch beim Experiment „Werfen einer Roulettekugel”.
$\text{Beispiel 9:}$ Ein weiteres Beispiel für ein vollständiges System ist die diskrete Zufallsgröße $X = \{ x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ mit den Auftrittswahrscheinlichkeiten entsprechend der folgenden Wahrscheinlichkeitsfunktion:
- $$P_X(X) = \big [ \hspace{0.1cm} P_X(x_1), P_X(x_2), \hspace{0.05cm}\text{...}\hspace{0.15cm}, P_X(x_I) \hspace{0.05cm} \big ] = \big [ \hspace{0.1cm} p_1, p_2, \hspace{0.05cm}\text{...} \hspace{0.15cm}, p_I \hspace{0.05cm} \big ] \hspace{0.05cm}$$
- $$\Rightarrow \hspace{0.3cm} p_1 = P_X(x_1) = {\rm Pr}(X=x_1) \hspace{0.05cm}, \hspace{0.2cm}p_2 = {\rm Pr}(X=x_2) \hspace{0.05cm},\hspace{0.05cm}\text{...}\hspace{0.15cm},\hspace{0.2cm} p_I = {\rm Pr}(X=x_I) \hspace{0.05cm}.$$
Die möglichen Ergebnisse $x_i$ der Zufallsgröße $X$ sind paarweise zueinander disjunkt und die Summe aller Auftrittswahrscheinlichkeiten $p_1 + p_2 + \hspace{0.1cm}\text{...}\hspace{0.1cm} + \hspace{0.05cm} p_I$ liefert grundsätzlich das Ergebnis $1$.
$\text{Beispiel 10:}$ Es gelte $X= \{0, 1, 2 \}$ und $P_X (X) = \big[0.2, \ 0.5, \ 0.3\big]$. Dann gilt:
- $${\rm Pr}(X=0) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=1) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=2) = 0.3 \hspace{0.05cm}.$$
Bei der Zufallsgröße $X = \{1, \pi, {\rm e} \}$ und gleichem $P_X(X) = \big[0.2, \ 0.5, \ 0.3\big]$ lauten die Zuordnungen:
- $${\rm Pr}(X=1) = 0.2 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X=\pi) = 0.5 \hspace{0.05cm}, \hspace{0.2cm} {\rm Pr}(X={\rm e}) = 0.3 \hspace{0.05cm}.$$
Hinweise:
- Die Wahrscheinlichkeitsfunktion $($englisch: "probability mass function", $\rm PMF)$ $P_X(X)$ macht nur Aussagen über die Wahrscheinlichkeiten, nicht über den Wertevorrat $\{x_1, x_2, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_I\}$ der Zufallsgröße $X$.
- Diese zusätzliche Information liefert die Wahrscheinlichkeitsdichtefunktion $\rm (WDF)$; englische Bezeichnung: "probability density function" $\rm (PDF)$.
Aufgaben zum Kapitel
Aufgabe 1.2: Schaltlogik (D/B-Wandler)
Aufgabe 1.3: Fiktive Uni Irgendwo
Aufgabe 1.3Z: Gewinnen mit Roulette?