Lineare zeitinvariante Systeme/Lineare Verzerrungen: Unterschied zwischen den Versionen
| (14 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
}} | }} | ||
==Zusammenstellung wichtiger Beschreibungsgrößen== | ==Zusammenstellung wichtiger Beschreibungsgrößen== | ||
| − | Nun werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird | + | <br> |
| − | + | [[Datei:P_ID899__LZI_T_2_3_S1_neu.png |frame|Lineare Systembeschreibung|class=fit]] | |
| − | + | Nun werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird. | |
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: | Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden: | ||
| − | $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot | + | :$$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot |
\hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} | ||
\hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$ | ||
Daraus ergeben sich folgende Beschreibungsgrößen: | Daraus ergeben sich folgende Beschreibungsgrößen: | ||
| − | *Der Betrag $|H(f)|$ wird als '''Amplitudengang''' und in logarithmierter Form als | + | *Der Betrag $|H(f)|$ wird als '''Amplitudengang''' und in logarithmierter Form als "Dämpfungsverlauf" bezeichnet: |
:$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | :$$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper | ||
\hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in | ||
\hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$ | \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$ | ||
| − | *Der '''Phasengang''' $b(f)$ gibt den negativen | + | *Der '''Phasengang''' $b(f)$ gibt den negativen, von $f$ abhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse: |
:$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | :$$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in | ||
\hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$ | ||
| − | == | + | ==Voraussetzungen für verzerrungsfreie Systeme== |
| − | Nach den Ausführungen im Kapitel [[Lineare_zeitinvariante_Systeme/Klassifizierung_der_Verzerrungen|Klassifizierung der Verzerrungen]] liegt genau dann ein verzerrungsfreies System vor, wenn alle Frequenzanteile gleichmäßig gedämpft und verzögert werden: | + | <br> |
| − | $$y(t) = \alpha \cdot x(t - \tau).$$ | + | Nach den Ausführungen im Kapitel [[Lineare_zeitinvariante_Systeme/Klassifizierung_der_Verzerrungen|Klassifizierung der Verzerrungen]] liegt genau dann ein verzerrungsfreies System vor, wenn alle Frequenzanteile gleichmäßig gedämpft und verzögert werden: |
| + | :$$y(t) = \alpha \cdot x(t - \tau).$$ | ||
Nach den Gesetzmäßigkeiten der Systemtheorie muss deshalb für den Frequenzgang | Nach den Gesetzmäßigkeiten der Systemtheorie muss deshalb für den Frequenzgang | ||
| − | $$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi f \tau}$$ | + | :$$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi \hspace{0.04cm} \cdot \hspace{0.04cm} f \hspace{0.04cm} \cdot \hspace{0.04cm} \tau}$$ |
| − | gelten, oder ausgedrückt mit den Funktionen $a(f)$ und $b(f)$: | + | gelten, oder ausgedrückt mit den Funktionen $a(f)$ und $b(f)$: |
*Der Dämpfungsverlauf muss für alle im Eingangssignal enthaltenen Frequenzen konstant sein: | *Der Dämpfungsverlauf muss für alle im Eingangssignal enthaltenen Frequenzen konstant sein: | ||
| − | :$$a(f) = - \ln |H(f)| = - \ln \alpha = {\rm const.}$$ | + | :$$a(f) = - \ln |H(f)| = - \ln \ \alpha = {\rm const.}$$ |
| − | *Der Phasenverlauf muss im interessierenden Bereich entweder | + | *Der Phasenverlauf muss im interessierenden Bereich entweder Null sein (System ohne Laufzeit) oder linear mit der Frequenz ansteigen $(τ$ gibt dabei die Laufzeit an): |
| − | :$$b(f) = 2 \pi f \tau = {\rm const.} \cdot f.$$ | + | :$$b(f) = 2 \pi \cdot f \cdot \tau = {\rm const.} \cdot f.$$ |
| − | Bei einem verzerrungsfreien System müssen beide Forderungen gleichzeitig erfüllt sein. Bei Verletzung auch nur einer dieser beiden Bedingungen kommt es zu linearen Verzerrungen, die entsprechend ihrer Ursache unterschieden werden. | + | {{BlaueBox|TEXT= |
| + | $\text{Definitionen:}$ | ||
| + | Bei einem verzerrungsfreien System müssen beide Forderungen gleichzeitig erfüllt sein. Bei Verletzung auch nur einer dieser beiden Bedingungen kommt es zu '''linearen Verzerrungen''', die entsprechend ihrer Ursache unterschieden werden. | ||
| + | *Es kommt zu '''Dämpfungsverzerrungen''', wenn im interessierenden Frequenzbereich der Dämpfungsverlauf nicht konstant ist: | ||
| + | :$$a(f) \ne {\rm const.}$$ | ||
| + | *Dagegen liegen '''Phasenverzerrungen''' dann vor, wenn die Phasenfunktion nicht linear bezüglich $f$ ist: | ||
| + | :$$b(f) \ne {\rm const.} \cdot f.$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Anzumerken ist, dass bei allen realisierbaren Systemen – insbesondere den im [[Lineare_zeitinvariante_Systeme/Folgerungen_aus_dem_Zuordnungssatz#D.C3.A4mpfung_und_Phase_von_Minimum.E2.80.93Phasen.E2.80.93Systemen|Kapitel 3]] beschriebenen „minimalphasigen Systemen” – meist Dämpfungsverzerrungen und Phasenverzerrungen gleichzeitig auftreten. | ||
| − | + | {{BlaueBox|TEXT= | |
| + | $\text{Definition:}$ Im Zeitbereich lautet die Bedingung für ein '''verzerrungsfreies System''': | ||
| + | :$$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$ | ||
| − | + | Ist zudem $α = 1$ und $τ = 0$, so liegt ein '''ideales Übertragungssystem''' vor. Dagegen gibt es immer dann lineare Verzerrungen, wenn | |
| − | + | *die Impulsantwort $h(t)$ eine zeitkontinuierliche Funktion ist, oder | |
| + | *die zeitdiskrete Impulsantwort $h(t)$ sich aus mehr als einer Diracfunktion zusammensetzt.}} | ||
| − | |||
| − | |||
| − | |||
| + | {{GraueBox|TEXT= | ||
| + | $\text{Beispiel 1:}$ | ||
| + | Die folgende Skizze zeigt den Dämpfungsverlauf $a(f)$ und den Phasenverlauf $b(f)$ eines verzerrungsfreien Systems. | ||
| + | [[Datei:P_ID900__LZI_T_2_3_S2_neu.png|right|frame| Voraussetzung für einen nichtverzerrenden Kanal|right|class=fit]] | ||
| − | {{ | + | *In einem Bereich von $f_{\rm U}$ bis $f_{\rm O}$ um die Trägerfrequenz $f_{\rm T}$, in dem das Signal $x(t)$ Anteile besitzt, ist $a(f)$ konstant. |
| − | Das | + | *Aus dem angegebenen konstanten Dämpfungswert $6 \ \rm dB$ folgt für den Amplitudengang: $\vert H(f)\vert = 0.5$. |
| − | + | * Das Ausgangsspektrum $Y(f)$ ist somit betragsmäßig halb so groß wie die Spektralanteile $X(f)$ des Eingangssignals. | |
| + | *Der Phasenverlauf $b(f)$ steigt zwischen $f_{\rm U}$ und $f_{\rm O}$ linear mit der Frequenz an. | ||
| + | *Dies hat zur Folge, dass alle Frequenzanteile um die gleiche Phasenlaufzeit $τ$ verzögert werden, wobei $τ$ durch die Steigung von $b(f)$ festliegt. | ||
| + | *Mit $b(f) = 0$ würde sich ein laufzeitfreies System ergeben ⇒ $τ = 0$. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Weiter erkennt man aus der Grafik folgende allgemeingültige Eigenschaften: | ||
| + | *Der Dämpfungsverlauf $a(f) = a(\hspace{-0.01cm}-\hspace{-0.08cm} f)$ ist eine gerade Funktion in $f$. | ||
| + | *Der Phasenverlauf $b(f) = \hspace{0.1cm}–\hspace{-0.01cm} b(\hspace{-0.01cm}-\hspace{-0.01cm}f)$ ist eine ungerade Funktion in $f$. | ||
| − | |||
| − | |||
| − | |||
| + | Außerhalb des durch $x(t)$ belegten Frequenzbandes müssen die Bedingungen „konstante Dämpfung” und „lineare Phase” nicht eingehalten werden. | ||
| − | + | Man erkennt aus dem gestrichelt eingezeichneten Verlauf von $a(f)$, dass hier sogar eine sehr viel höhere Dämpfung zweckmäßig ist, da dadurch die stets vorhandenen – in diesem Abschnitt aber nicht betrachteten – Rauschanteile außerhalb der Nutzbandbreite besser unterdrückt werden. }} | |
| − | |||
==Dämpfungsverzerrungen== | ==Dämpfungsverzerrungen== | ||
| + | <br> | ||
Wir betrachten im Folgenden als Eingangssignal die Summe zweier harmonischer Schwingungen: | Wir betrachten im Folgenden als Eingangssignal die Summe zweier harmonischer Schwingungen: | ||
| − | $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | + | :$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - |
\varphi_2).$$ | \varphi_2).$$ | ||
| − | Ist das Ausgangssignal in der Form | + | *Ist das Ausgangssignal in der Form |
| − | $$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - | + | :$$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - |
\varphi_2).$$ | \varphi_2).$$ | ||
| − | darstellbar und gilt | + | :darstellbar und gilt $α_1 ≠ α_2$, so liegen '''ausschließlich Dämpfungsverzerrungen''' vor. Die Phasenwerte $\varphi_1$ und $\varphi_2$ werden durch das System nicht verändert. |
| − | Die Dämpfungskonstanten $α_1$ und $α_2$ können aus dem Amplitudengang $|H(f)|$ ermittelt werden: | + | *Die Dämpfungskonstanten $α_1$ und $α_2$ können aus dem Amplitudengang $|H(f)|$ ermittelt werden: |
| − | $$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$ | + | :$$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$ |
| − | Ist der Dämpfungsverlauf $a(f)$ in Neper gegeben, so gilt gleichermaßen ( | + | *Ist der Dämpfungsverlauf $a(f)$ in Neper gegeben, so gilt gleichermaßen $(1 \ \rm dB$ entspricht $0.1151 \ \rm Np)$: |
| − | $$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$ | + | :$$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$ |
| − | + | Hinweis: Bei manchen Zeichenfonts sind „$a$” und „$α$” (alpha) schwer zu unterscheiden. | |
| − | + | [[Datei:P_ID901__LZI_T_2_3_S3_neu.png |frame| Auswirkungen von Dämpfungsverzerrungen | right|class=fit]] | |
| − | [[Datei:P_ID901__LZI_T_2_3_S3_neu.png | Auswirkungen von Dämpfungsverzerrungen | right|class=fit]] | + | {{GraueBox|TEXT= |
| + | $\text{Beispiel 2:}$ | ||
| + | Die Grafik zeigt das mit $T_0 = 1\ \rm ms$ periodische Eingangssignal ⇒ blauer Kurvenverlauf, | ||
| + | :$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | ||
| + | und das mit $α_1 = 0.2$, $α_2 = 0.5$ dämpfungsverzerrte Signal $y(t)$ ⇒ roter Kurvenverlauf. | ||
| − | + | Man erkennt signifikante Auswirkungen dieser Dämpfungsverzerrungen: | |
| − | + | *$y(t)$ hat nur noch wenig Ähnlichkeit mit $x(t)$. | |
| − | + | *Dagegen würde sich mit $α_1 = α_2 = α$ das verzerrungsfreie Signal $y(t) = α · x(t)$ ergeben, aus dem man durch Verstärkung um $1/α$ das ursprüngliche Signal $x(t)$ wieder rekonstruieren könnte. | |
| − | Man erkennt | ||
| − | *$y(t)$ hat nur noch wenig Ähnlichkeit mit $x(t)$. | ||
| − | *Dagegen würde sich mit $α_1 = α_2 = α$ das verzerrungsfreie Signal $y(t) = α · x(t)$ ergeben, aus dem durch Verstärkung um $1/α$ das ursprüngliche Signal $x(t)$ wieder | ||
| − | |||
| − | + | Wir weisen hier ausdrücklich auf das interaktive Applet [[Applets:Lineare_Verzerrungen_periodischer_Signale|Lineare Verzerrungen periodischer Signale]] hin.}} | |
| − | |||
==Phasenlaufzeit== | ==Phasenlaufzeit== | ||
| − | Wir betrachten ein System mit $|H(f)| = 1$, so dass für den Frequenzgang gilt: | + | <br> |
| − | $$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} | + | Wir betrachten ein System mit $|H(f)| = 1$, so dass für den Frequenzgang gilt: |
| + | :$$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} | ||
b(f)}.$$ | b(f)}.$$ | ||
| − | Die linke Grafik zeigt einen beispielhaften Phasenverlauf $b(f)$. | + | *Die linke Grafik zeigt einen beispielhaften Phasenverlauf $b(f)$. Ein solcher Phasenverlauf ist stets eine ungerade Funktion bezüglich der Frequenz: $b(\hspace{-0.01cm}-\hspace{-0.08cm}f) = \hspace{0.08cm}-b(f)$. |
| + | *Rechts ist die Funktion $b(ω)$ skizziert, die gegenüber $b(f)$ in der Abszisse um den Faktor $2π$ gestreckt ist. | ||
| − | |||
| − | |||
| − | |||
Liegt am Eingang die harmonische Schwingung | Liegt am Eingang die harmonische Schwingung | ||
| − | $$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi) | + | :$$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi) \hspace{0.15cm} |
| − | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, X(f ) = {C}/{2}\cdot | + | \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.15cm} X(f ) = {C}/{2}\cdot |
| − | {\rm e}^{{\rm j}\hspace{0. | + | {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f + f_0) |
\hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm | \hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm | ||
| − | j}\hspace{0. | + | j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f - f_0)$$ |
| − | an, so ergibt sich für die Spektralfunktion am Ausgang | + | [[Datei: P_ID902__LZI_T_2_3_S4_neu.png |frame|Zur Definition der Phasenlaufzeit|class=fit]] |
| − | $$Y(f ) = {C}/{2}\cdot | + | |
| − | {\rm e}^{{\rm j}\hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm | + | an, so ergibt sich für die Spektralfunktion am Ausgang: |
| − | j}\hspace{0.05cm} b(f_0)} \cdot \delta(f + f_0) \hspace{0.05cm} + | + | :$$Y(f ) = {C}/{2}\cdot |
| − | \hspace{0.05cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} | + | {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm |
| − | \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} b(f_0)} \cdot | + | j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot \delta(f + f_0) \hspace{0.05cm} + |
| + | \hspace{0.05cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} | ||
| + | \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot | ||
\delta(f - f_0).$$ | \delta(f - f_0).$$ | ||
Somit lautet das Ausgangssignal: | Somit lautet das Ausgangssignal: | ||
| − | $$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$ | + | :$$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$ |
| − | Dieses kann auch in folgender Form dargestellt werden: | + | Dieses Signal kann auch in folgender Form dargestellt werden: |
| − | $$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$ | + | :$$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$ |
| + | <br clear=all> | ||
| + | {{BlaueBox|TEXT= | ||
| + | $\text{Definition:}$ | ||
| + | Die '''Phasenlaufzeit''' gibt die Verzögerung an, die eine harmonische Schwingung mit der Frequenz $f_0$ durch das System erfährt. | ||
| + | *Bei phasenverzerrenden Systemen ist die Phasenlaufzeit frequenzabhängig: | ||
| + | :$$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm bzw.} \hspace{0.4cm} | ||
| + | \tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Zu dieser Definition ist anzumerken: | ||
| + | *In der $b(ω)$–Darstellung kann die Phasenlaufzeit $τ_{\rm P}$ als die Steigung der in der obigen Grafik grün eingezeichneten Geraden auch grafisch ermittelt werden. | ||
| + | *Im Allgemeinen wird eine Schwingung anderer Frequenz eine andere Phasenlaufzeit zur Folge haben. Dies ist der physikalische Hintergrund für Phasenverzerrungen. | ||
| + | *Gilt bei einem System $b(ω) = τ_{\rm P} · ω$ bzw. $b(f) = 2π · τ_{\rm P} · f$, so haben alle Frequenzen die gleiche Phasenlaufzeit $τ_{\rm P}$. <br>Ein solches System führt nicht zu Phasenverzerrungen. | ||
| − | + | ||
| − | + | Wir verweisen hier nochmals auf das interaktive Applet [[Applets:Lineare_Verzerrungen_periodischer_Signale|Lineare Verzerrungen periodischer Signale]]. | |
| − | |||
| − | |||
==Unterschied zwischen Phasen- und Gruppenlaufzeit== | ==Unterschied zwischen Phasen- und Gruppenlaufzeit== | ||
| + | <br> | ||
| + | Eine weitere wichtige Systembeschreibungsgröße ist die Gruppenlaufzeit, die nicht mit der Phasenlaufzeit verwechselt werden darf. | ||
| − | + | {{BlaueBox|TEXT= | |
| − | + | $\text{Definition:}$ | |
| − | + | Die '''Gruppenlaufzeit''' ist wie folgt definiert: | |
| − | Die '''Gruppenlaufzeit''' ist wie folgt definiert: | + | :$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0}.$$ |
| − | $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0}.$$ | + | *Diese Größe wird vorwiegend zur Beschreibung von Schmalbandsystemen herangezogen. |
| − | + | *Sie gibt die Verzögerung an, welche die Hüllkurve eines Bandpass–Systems erfährt. }} | |
| − | Diese Größe wird vorwiegend zur Beschreibung von Schmalbandsystemen herangezogen. Sie gibt die Verzögerung an, welche die Hüllkurve eines Bandpass | ||
| − | |||
| − | + | [[Datei: P_ID904__LZI_T_2_3_S5_neu.png| right|frame|Zur Definition der Gruppenlaufzeit|class=fit]] | |
| − | [[Datei: P_ID904__LZI_T_2_3_S5_neu.png| right|Zur Definition der Gruppenlaufzeit|class=fit]] | + | {{GraueBox|TEXT= |
| − | Die Grafik zeigt die beispielhafte Phasenfunktion $b(ω) = \arctan (ω/ω_0)$ | + | $\text{Beispiel 3:}$ |
| − | *Diese steigt monoton von $ | + | Die Grafik zeigt die beispielhafte Phasenfunktion: |
| − | *Der Funktionswert bei $ω = ω_0$ beträgt $π/4$. | + | :$$b(ω) = \arctan (ω/ω_0).$$ |
| + | *Diese steigt monoton von Null $($bei $ω = 0)$ bis $π/2$ $($für $ω → ∞)$. | ||
| + | *Der Funktionswert bei $ω = ω_0$ beträgt $π/4$. | ||
| − | Setzen wir $ω_0 = 2π · 1 \ \rm kHz$, so erhalten wir für die ''Phasenlaufzeit:'' | + | Setzen wir $ω_0 = 2π · 1 \ \rm kHz$, so erhalten wir für die '''Phasenlaufzeit:''' |
| − | $$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz}} = {125\, \rm | + | :$$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz} } = {125\, \rm µ s}.$$ |
| − | Diese Größe entspricht der Steigung der grün eingezeichneten Geraden in | + | Diese Größe entspricht der Steigung der grün eingezeichneten Geraden in obiger Grafik. |
| − | Dagegen kennzeichnet die geringere Steigung der rot dargestellten Tangente die ''Gruppenlaufzeit:'' | + | Dagegen kennzeichnet die geringere Steigung der rot dargestellten Tangente die '''Gruppenlaufzeit:''' |
| − | $$\tau_{\rm G}(\omega_0) = \left[ \frac{{\rm d}b(\omega)}{{\rm d}\omega}\right ]_{\omega = \omega_0} = | + | :$$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0} = |
\left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = | \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = | ||
\omega_0} | \omega_0} | ||
| − | = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz}} | + | = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz} } |
| − | \approx {80\, \rm | + | \approx {80\, \rm µ s}.$$}} |
| − | |||
| − | |||
| − | |||
==Phasenverzerrungen== | ==Phasenverzerrungen== | ||
| + | <br> | ||
Zur Verdeutlichung dieses Sachverhaltes betrachten wir als Eingangssignal wieder die Summe zweier harmonischer Schwingungen: | Zur Verdeutlichung dieses Sachverhaltes betrachten wir als Eingangssignal wieder die Summe zweier harmonischer Schwingungen: | ||
| − | $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - | + | :$$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - |
\varphi_2).$$ | \varphi_2).$$ | ||
| − | Ist bei diesem Eingangssignal das Ausgangssignal in der Form | + | *Ist bei diesem Eingangssignal das Ausgangssignal in der Form |
| − | $$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - | + | :$$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - |
\varphi_2)$$ | \varphi_2)$$ | ||
| − | darstellbar und gilt gleichzeitig $τ_1 ≠ τ_2$, so liegen '''ausschließlich Phasenverzerrungen''' vor. | + | :darstellbar und gilt gleichzeitig $τ_1 ≠ τ_2$, so liegen '''ausschließlich Phasenverzerrungen''' vor. |
| − | Die beiden Phasenlaufzeiten $τ_1 ≠ τ_2$ können aus dem Phasenverlauf in Radian ermittelt werden: | + | *Die beiden Phasenlaufzeiten $τ_1 ≠ τ_2$ können aus dem Phasenverlauf (in Radian) ermittelt werden: |
| − | $$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi | + | :$$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi |
f_2}.$$ | f_2}.$$ | ||
| − | {{Beispiel} | + | [[Datei: P_ID905__LZI_T_2_3_S6_neu.png|right|frame|Auswirkungen von Phasenverzerrungen|class=fit]] |
| − | Die Grafik zeigt als blauen Kurvenverlauf das mit der Periodendauer $T_0$ periodische Signal | + | {{GraueBox|TEXT= |
| − | $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | + | $\text{Beispiel 4:}$ |
| − | sowie das mit den Laufzeiten $τ_1 = 0.7 \ \rm ms$ und $τ_2 = 0.3 \ \rm ms$ phasenverzerrte | + | Die Grafik zeigt als blauen Kurvenverlauf das mit der Periodendauer $T_0$ periodische Signal |
| + | :$$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$ | ||
| + | sowie das mit den Laufzeiten $τ_1 = 0.7 \ \rm ms$ und $τ_2 = 0.3 \ \rm ms$ phasenverzerrte Ausgangssignal $y(t)$ ⇒ roter Kurvenverlauf. | ||
| + | *Man erkennt an den beiden Signalverläufen deutlich die Auswirkungen der Phasenverzerrungen. | ||
| − | + | *Mit $τ_1 = τ_2 = τ$ ergäbe sich das verzerrungsfreie Signal | |
| + | :$$y(t) = x(t - τ).$$ | ||
| − | |||
| − | |||
| + | Wir weisen nochmals auf das interaktive Applet [[Applets:Lineare_Verzerrungen_periodischer_Signale|Lineare Verzerrungen periodischer Signale]] hin.}} | ||
| − | |||
| − | |||
==Entzerrungsverfahren== | ==Entzerrungsverfahren== | ||
| − | Dieses für die Nachrichtentechnik sehr wichtige Verfahren soll hier nur kurz angerissen werden. Nähere Informationen hierzu finden Sie in den Büchern [[Modulationsverfahren|Modulationsverfahren]] und [[Digitalsignalübertragung|Digitalsignalübertragung]]. | + | <br> |
| + | [[Datei:P_ID906__LZI_T_2_3_S7_neu.png|right|frame| Entzerrung von Signalen|class=fit]] | ||
| + | Dieses für die Nachrichtentechnik sehr wichtige Verfahren soll hier nur kurz angerissen werden. Nähere Informationen hierzu finden Sie in den Büchern [[Modulationsverfahren|Modulationsverfahren]] und [[Digitalsignalübertragung|Digitalsignalübertragung]]. | ||
| − | Wir gehen für diese Kurzbeschreibung von | + | Wir gehen für diese Kurzbeschreibung von der skizzierten Konstellation aus: |
| + | *$S_{\rm V}$ bezeichnet ein verzerrendes System, | ||
| + | *während $S_{\rm E}$ der Entzerrung dient. | ||
| − | |||
| − | + | Zu dieser Konstellation ist anzumerken: | |
| − | *Ist die Verzerrung | + | *Ist die Verzerrung nichtlinear, so muss auch die Entzerrung nichtlinear erfolgen. |
| − | *Aber auch bei linearen Verzerrungen werden nichtlineare Entzerrungsverfahren eingesetzt, zum Beispiel | + | *Aber auch bei linearen Verzerrungen werden nichtlineare Entzerrungsverfahren eingesetzt, zum Beispiel "Decision Feedback Equalization" bei Digitalsystemen. Der Vorteil gegenüber linearer Entzerrung ist, dass es nicht zu einer Erhöhung der Rauschleistung kommt. |
| − | *Ist $S_{\rm V}$ ein lineares System mit Frequenzgang $H_{\rm V}(f)$, so können mit dem ''inversen Frequenzgang'' $H_{\rm E}(f) = 1/H_{\rm V}(f)$ die Verzerrungen vollständig eliminiert werden, und es gilt $z(t) = x(t)$. | + | *Ist $S_{\rm V}$ ein lineares System mit Frequenzgang $H_{\rm V}(f)$, so können mit dem '''inversen Frequenzgang''' $H_{\rm E}(f) = 1/H_{\rm V}(f)$ die Verzerrungen vollständig eliminiert werden, und es gilt $z(t) = x(t)$. Voraussetzung hierfür ist allerdings, dass der Frequenzgang $H_{\rm V}(f)$ im interessierenden Spektralbereich keine Nullstellen besitzt, da sonst bei $H_{\rm E}(f)$ Unendlichkeitsstellen erforderlich wären. |
| − | + | *Bei '''Analogsystemen''' bedeutet eine vollständige Entzerrung, dass sich $z(t)$ von $x(t)$ nur durch die unvermeidbaren Rauschanteile unterscheidet, und eventuell durch eine Laufzeit. Bei '''Digitalsystemen''' ist das Kriterium für eine vollständige Entzerrung weniger streng. Es muss dann nur sichergestellt werden, dass die Signale $x(t)$ und $z(t)$ zu den Detektionszeitpunkten übereinstimmen. Man spricht in diesem Zusammenhang von [[Digitalsignalübertragung/Eigenschaften_von_Nyquistsystemen|Nyquistsystemen]]. | |
| − | *Bei ''Analogsystemen'' bedeutet eine vollständige Entzerrung, dass sich $z(t)$ von $x(t)$ nur durch die unvermeidbaren Rauschanteile unterscheidet, und eventuell durch eine Laufzeit. | ||
| − | |||
==Aufgaben zum Kapitel== | ==Aufgaben zum Kapitel== | ||
| + | <br> | ||
| + | [[Aufgaben:2.5_Verzerrung_und_Entzerrung|Aufgabe 2.5: Verzerrung und Entzerrung]] | ||
| − | [[Aufgaben: | + | [[Aufgaben:Aufgabe_2.5Z:_Nyquistentzerrung|Aufgabe 2.5Z: Nyquistentzerrung]] |
| − | [[2. | + | [[Aufgaben:2.6_Zweiwegekanal|Aufgabe 2.6: Zweiwegekanal]] |
| − | [[Aufgaben:2. | + | [[Aufgaben:2.6Z_Synchrondemodulator|Aufgabe 2.6Z: Synchrondemodulator]] |
| − | [[2. | + | [[Aufgaben:2.7_Nochmals_Zweiwegekanal|Aufgabe 2.7: Nochmals Zweiwegekanal]] |
{{Display}} | {{Display}} | ||
Aktuelle Version vom 5. Oktober 2021, 14:28 Uhr
Inhaltsverzeichnis
Zusammenstellung wichtiger Beschreibungsgrößen
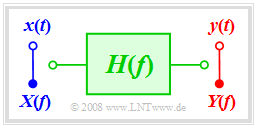
Nun werden nichtlineare Verzerrungen ausgeschlossen, so dass das System durch den Frequenzgang $H(f)$ vollständig beschrieben wird.
Der im Allgemeinen komplexe Frequenzgang kann auch wie folgt dargestellt werden:
- $$H(f) = |H(f)| \cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)} = {\rm e}^{-a(f)}\cdot {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
Daraus ergeben sich folgende Beschreibungsgrößen:
- Der Betrag $|H(f)|$ wird als Amplitudengang und in logarithmierter Form als "Dämpfungsverlauf" bezeichnet:
- $$a(f) = - \ln |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Neper \hspace{0.1cm}(Np) } = - 20 \cdot \lg |H(f)|\hspace{0.2cm}{\rm in \hspace{0.1cm}Dezibel \hspace{0.1cm}(dB) }.$$
- Der Phasengang $b(f)$ gibt den negativen, von $f$ abhängigen Winkel von $H(f)$ in der komplexen Ebene an, bezogen auf die reelle Achse:
- $$b(f) = - {\rm arc} \hspace{0.1cm}H(f) \hspace{0.2cm}{\rm in \hspace{0.1cm}Radian \hspace{0.1cm}(rad)}.$$
Voraussetzungen für verzerrungsfreie Systeme
Nach den Ausführungen im Kapitel Klassifizierung der Verzerrungen liegt genau dann ein verzerrungsfreies System vor, wenn alle Frequenzanteile gleichmäßig gedämpft und verzögert werden:
- $$y(t) = \alpha \cdot x(t - \tau).$$
Nach den Gesetzmäßigkeiten der Systemtheorie muss deshalb für den Frequenzgang
- $$H(f) = \alpha \cdot {\rm e}^{-{\rm j}\hspace{0.04cm}2 \pi \hspace{0.04cm} \cdot \hspace{0.04cm} f \hspace{0.04cm} \cdot \hspace{0.04cm} \tau}$$
gelten, oder ausgedrückt mit den Funktionen $a(f)$ und $b(f)$:
- Der Dämpfungsverlauf muss für alle im Eingangssignal enthaltenen Frequenzen konstant sein:
- $$a(f) = - \ln |H(f)| = - \ln \ \alpha = {\rm const.}$$
- Der Phasenverlauf muss im interessierenden Bereich entweder Null sein (System ohne Laufzeit) oder linear mit der Frequenz ansteigen $(τ$ gibt dabei die Laufzeit an):
- $$b(f) = 2 \pi \cdot f \cdot \tau = {\rm const.} \cdot f.$$
$\text{Definitionen:}$ Bei einem verzerrungsfreien System müssen beide Forderungen gleichzeitig erfüllt sein. Bei Verletzung auch nur einer dieser beiden Bedingungen kommt es zu linearen Verzerrungen, die entsprechend ihrer Ursache unterschieden werden.
- Es kommt zu Dämpfungsverzerrungen, wenn im interessierenden Frequenzbereich der Dämpfungsverlauf nicht konstant ist:
- $$a(f) \ne {\rm const.}$$
- Dagegen liegen Phasenverzerrungen dann vor, wenn die Phasenfunktion nicht linear bezüglich $f$ ist:
- $$b(f) \ne {\rm const.} \cdot f.$$
Anzumerken ist, dass bei allen realisierbaren Systemen – insbesondere den im Kapitel 3 beschriebenen „minimalphasigen Systemen” – meist Dämpfungsverzerrungen und Phasenverzerrungen gleichzeitig auftreten.
$\text{Definition:}$ Im Zeitbereich lautet die Bedingung für ein verzerrungsfreies System:
- $$h(t) = \alpha \cdot \delta(t - \tau),\hspace{0.4cm}\alpha \ne 0.$$
Ist zudem $α = 1$ und $τ = 0$, so liegt ein ideales Übertragungssystem vor. Dagegen gibt es immer dann lineare Verzerrungen, wenn
- die Impulsantwort $h(t)$ eine zeitkontinuierliche Funktion ist, oder
- die zeitdiskrete Impulsantwort $h(t)$ sich aus mehr als einer Diracfunktion zusammensetzt.
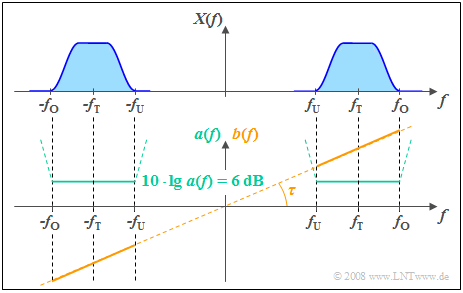
$\text{Beispiel 1:}$ Die folgende Skizze zeigt den Dämpfungsverlauf $a(f)$ und den Phasenverlauf $b(f)$ eines verzerrungsfreien Systems.
- In einem Bereich von $f_{\rm U}$ bis $f_{\rm O}$ um die Trägerfrequenz $f_{\rm T}$, in dem das Signal $x(t)$ Anteile besitzt, ist $a(f)$ konstant.
- Aus dem angegebenen konstanten Dämpfungswert $6 \ \rm dB$ folgt für den Amplitudengang: $\vert H(f)\vert = 0.5$.
- Das Ausgangsspektrum $Y(f)$ ist somit betragsmäßig halb so groß wie die Spektralanteile $X(f)$ des Eingangssignals.
- Der Phasenverlauf $b(f)$ steigt zwischen $f_{\rm U}$ und $f_{\rm O}$ linear mit der Frequenz an.
- Dies hat zur Folge, dass alle Frequenzanteile um die gleiche Phasenlaufzeit $τ$ verzögert werden, wobei $τ$ durch die Steigung von $b(f)$ festliegt.
- Mit $b(f) = 0$ würde sich ein laufzeitfreies System ergeben ⇒ $τ = 0$.
Weiter erkennt man aus der Grafik folgende allgemeingültige Eigenschaften:
- Der Dämpfungsverlauf $a(f) = a(\hspace{-0.01cm}-\hspace{-0.08cm} f)$ ist eine gerade Funktion in $f$.
- Der Phasenverlauf $b(f) = \hspace{0.1cm}–\hspace{-0.01cm} b(\hspace{-0.01cm}-\hspace{-0.01cm}f)$ ist eine ungerade Funktion in $f$.
Außerhalb des durch $x(t)$ belegten Frequenzbandes müssen die Bedingungen „konstante Dämpfung” und „lineare Phase” nicht eingehalten werden.
Man erkennt aus dem gestrichelt eingezeichneten Verlauf von $a(f)$, dass hier sogar eine sehr viel höhere Dämpfung zweckmäßig ist, da dadurch die stets vorhandenen – in diesem Abschnitt aber nicht betrachteten – Rauschanteile außerhalb der Nutzbandbreite besser unterdrückt werden.
Dämpfungsverzerrungen
Wir betrachten im Folgenden als Eingangssignal die Summe zweier harmonischer Schwingungen:
- $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
- Ist das Ausgangssignal in der Form
- $$y(t) = \alpha_1 \cdot A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + \alpha_2 \cdot A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
- darstellbar und gilt $α_1 ≠ α_2$, so liegen ausschließlich Dämpfungsverzerrungen vor. Die Phasenwerte $\varphi_1$ und $\varphi_2$ werden durch das System nicht verändert.
- Die Dämpfungskonstanten $α_1$ und $α_2$ können aus dem Amplitudengang $|H(f)|$ ermittelt werden:
- $$\alpha_1 = |H(f_1)|,\hspace{0.4cm}\alpha_2 = |H(f_2)|.$$
- Ist der Dämpfungsverlauf $a(f)$ in Neper gegeben, so gilt gleichermaßen $(1 \ \rm dB$ entspricht $0.1151 \ \rm Np)$:
- $$ \alpha_1 = {\rm e}^{-{\rm a}(f_1)},\hspace{0.4cm}\alpha_2 = {\rm e}^{-{\rm a}(f_2)}.$$
Hinweis: Bei manchen Zeichenfonts sind „$a$” und „$α$” (alpha) schwer zu unterscheiden.
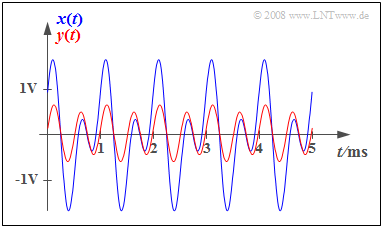
$\text{Beispiel 2:}$ Die Grafik zeigt das mit $T_0 = 1\ \rm ms$ periodische Eingangssignal ⇒ blauer Kurvenverlauf,
- $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$
und das mit $α_1 = 0.2$, $α_2 = 0.5$ dämpfungsverzerrte Signal $y(t)$ ⇒ roter Kurvenverlauf.
Man erkennt signifikante Auswirkungen dieser Dämpfungsverzerrungen:
- $y(t)$ hat nur noch wenig Ähnlichkeit mit $x(t)$.
- Dagegen würde sich mit $α_1 = α_2 = α$ das verzerrungsfreie Signal $y(t) = α · x(t)$ ergeben, aus dem man durch Verstärkung um $1/α$ das ursprüngliche Signal $x(t)$ wieder rekonstruieren könnte.
Wir weisen hier ausdrücklich auf das interaktive Applet Lineare Verzerrungen periodischer Signale hin.
Phasenlaufzeit
Wir betrachten ein System mit $|H(f)| = 1$, so dass für den Frequenzgang gilt:
- $$H(f) = {\rm e}^{-{\rm j} \hspace{0.05cm} \cdot \hspace{0.05cm} b(f)}.$$
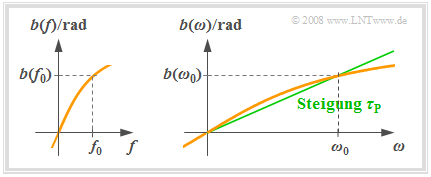
- Die linke Grafik zeigt einen beispielhaften Phasenverlauf $b(f)$. Ein solcher Phasenverlauf ist stets eine ungerade Funktion bezüglich der Frequenz: $b(\hspace{-0.01cm}-\hspace{-0.08cm}f) = \hspace{0.08cm}-b(f)$.
- Rechts ist die Funktion $b(ω)$ skizziert, die gegenüber $b(f)$ in der Abszisse um den Faktor $2π$ gestreckt ist.
Liegt am Eingang die harmonische Schwingung
- $$x(t) = C \cdot \cos(2 \pi f_0 t - \varphi) \hspace{0.15cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.15cm} X(f ) = {C}/{2}\cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f + f_0) \hspace{0.01cm} + \hspace{0.01cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot \delta(f - f_0)$$
an, so ergibt sich für die Spektralfunktion am Ausgang:
- $$Y(f ) = {C}/{2}\cdot {\rm e}^{{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot \delta(f + f_0) \hspace{0.05cm} + \hspace{0.05cm}{C}/{2}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} \varphi}\cdot {\rm e}^{-{\rm j}\hspace{0.05cm} \cdot \hspace{0.05cm} b(f_0)} \cdot \delta(f - f_0).$$
Somit lautet das Ausgangssignal:
- $$y(t) = C \cdot \cos(2 \pi f_0 t - b(f_0) - \varphi).$$
Dieses Signal kann auch in folgender Form dargestellt werden:
- $$y(t) = C \cdot \cos(2 \pi f_0 ( t - \tau_{\rm P}(f_0)) - \varphi).$$
$\text{Definition:}$ Die Phasenlaufzeit gibt die Verzögerung an, die eine harmonische Schwingung mit der Frequenz $f_0$ durch das System erfährt.
- Bei phasenverzerrenden Systemen ist die Phasenlaufzeit frequenzabhängig:
- $$\tau_{\rm P}(f_0) = \frac{b(f_0)}{2\pi f_0} \hspace{0.4cm}{\rm bzw.} \hspace{0.4cm} \tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}.$$
Zu dieser Definition ist anzumerken:
- In der $b(ω)$–Darstellung kann die Phasenlaufzeit $τ_{\rm P}$ als die Steigung der in der obigen Grafik grün eingezeichneten Geraden auch grafisch ermittelt werden.
- Im Allgemeinen wird eine Schwingung anderer Frequenz eine andere Phasenlaufzeit zur Folge haben. Dies ist der physikalische Hintergrund für Phasenverzerrungen.
- Gilt bei einem System $b(ω) = τ_{\rm P} · ω$ bzw. $b(f) = 2π · τ_{\rm P} · f$, so haben alle Frequenzen die gleiche Phasenlaufzeit $τ_{\rm P}$.
Ein solches System führt nicht zu Phasenverzerrungen.
Wir verweisen hier nochmals auf das interaktive Applet Lineare Verzerrungen periodischer Signale.
Unterschied zwischen Phasen- und Gruppenlaufzeit
Eine weitere wichtige Systembeschreibungsgröße ist die Gruppenlaufzeit, die nicht mit der Phasenlaufzeit verwechselt werden darf.
$\text{Definition:}$ Die Gruppenlaufzeit ist wie folgt definiert:
- $$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0}.$$
- Diese Größe wird vorwiegend zur Beschreibung von Schmalbandsystemen herangezogen.
- Sie gibt die Verzögerung an, welche die Hüllkurve eines Bandpass–Systems erfährt.
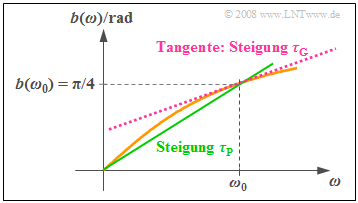
$\text{Beispiel 3:}$ Die Grafik zeigt die beispielhafte Phasenfunktion:
- $$b(ω) = \arctan (ω/ω_0).$$
- Diese steigt monoton von Null $($bei $ω = 0)$ bis $π/2$ $($für $ω → ∞)$.
- Der Funktionswert bei $ω = ω_0$ beträgt $π/4$.
Setzen wir $ω_0 = 2π · 1 \ \rm kHz$, so erhalten wir für die Phasenlaufzeit:
- $$\tau_{\rm P}(\omega_0) = \frac{b(\omega_0)}{\omega_0}= \frac{\pi / 4}{2 \pi \cdot{1\, \rm kHz} } = {125\, \rm µ s}.$$
Diese Größe entspricht der Steigung der grün eingezeichneten Geraden in obiger Grafik.
Dagegen kennzeichnet die geringere Steigung der rot dargestellten Tangente die Gruppenlaufzeit:
- $$\tau_{\rm G}(\omega_0) = \left[ \frac{ {\rm d}b(\omega)}{ {\rm d}\omega}\right ]_{\omega = \omega_0} = \left[ \frac{1}{\omega_0} \cdot \frac{1}{1 + \left(\omega / \omega_0\right]^2} \right ]_{\omega = \omega_0} = \frac{1}{2\omega_0}= \frac{1}{4 \pi \cdot{1\, \rm kHz} } \approx {80\, \rm µ s}.$$
Phasenverzerrungen
Zur Verdeutlichung dieses Sachverhaltes betrachten wir als Eingangssignal wieder die Summe zweier harmonischer Schwingungen:
- $$x(t) = A_1 \cdot \cos(2 \pi f_1 \cdot t - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot t - \varphi_2).$$
- Ist bei diesem Eingangssignal das Ausgangssignal in der Form
- $$y(t) = A_1 \cdot \cos(2 \pi f_1 \cdot (t - \tau_1) - \varphi_1) + A_2 \cdot \cos(2 \pi f_2 \cdot (t - \tau_2) - \varphi_2)$$
- darstellbar und gilt gleichzeitig $τ_1 ≠ τ_2$, so liegen ausschließlich Phasenverzerrungen vor.
- Die beiden Phasenlaufzeiten $τ_1 ≠ τ_2$ können aus dem Phasenverlauf (in Radian) ermittelt werden:
- $$\tau_1 = \frac{b(f_1)}{2\pi f_1} , \hspace{0.4cm}\tau_2 = \frac{b(f_2)}{2\pi f_2}.$$
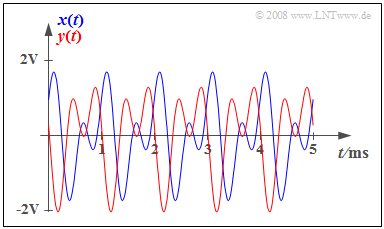
$\text{Beispiel 4:}$ Die Grafik zeigt als blauen Kurvenverlauf das mit der Periodendauer $T_0$ periodische Signal
- $$x(t) = {1\, \rm V} \cdot \cos(2 \pi \cdot {1\, \rm kHz}\cdot t) + {1\, \rm V} \cdot \sin(2 \pi \cdot {2\, \rm kHz}\cdot t)$$
sowie das mit den Laufzeiten $τ_1 = 0.7 \ \rm ms$ und $τ_2 = 0.3 \ \rm ms$ phasenverzerrte Ausgangssignal $y(t)$ ⇒ roter Kurvenverlauf.
- Man erkennt an den beiden Signalverläufen deutlich die Auswirkungen der Phasenverzerrungen.
- Mit $τ_1 = τ_2 = τ$ ergäbe sich das verzerrungsfreie Signal
- $$y(t) = x(t - τ).$$
Wir weisen nochmals auf das interaktive Applet Lineare Verzerrungen periodischer Signale hin.
Entzerrungsverfahren
Dieses für die Nachrichtentechnik sehr wichtige Verfahren soll hier nur kurz angerissen werden. Nähere Informationen hierzu finden Sie in den Büchern Modulationsverfahren und Digitalsignalübertragung.
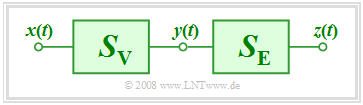
Wir gehen für diese Kurzbeschreibung von der skizzierten Konstellation aus:
- $S_{\rm V}$ bezeichnet ein verzerrendes System,
- während $S_{\rm E}$ der Entzerrung dient.
Zu dieser Konstellation ist anzumerken:
- Ist die Verzerrung nichtlinear, so muss auch die Entzerrung nichtlinear erfolgen.
- Aber auch bei linearen Verzerrungen werden nichtlineare Entzerrungsverfahren eingesetzt, zum Beispiel "Decision Feedback Equalization" bei Digitalsystemen. Der Vorteil gegenüber linearer Entzerrung ist, dass es nicht zu einer Erhöhung der Rauschleistung kommt.
- Ist $S_{\rm V}$ ein lineares System mit Frequenzgang $H_{\rm V}(f)$, so können mit dem inversen Frequenzgang $H_{\rm E}(f) = 1/H_{\rm V}(f)$ die Verzerrungen vollständig eliminiert werden, und es gilt $z(t) = x(t)$. Voraussetzung hierfür ist allerdings, dass der Frequenzgang $H_{\rm V}(f)$ im interessierenden Spektralbereich keine Nullstellen besitzt, da sonst bei $H_{\rm E}(f)$ Unendlichkeitsstellen erforderlich wären.
- Bei Analogsystemen bedeutet eine vollständige Entzerrung, dass sich $z(t)$ von $x(t)$ nur durch die unvermeidbaren Rauschanteile unterscheidet, und eventuell durch eine Laufzeit. Bei Digitalsystemen ist das Kriterium für eine vollständige Entzerrung weniger streng. Es muss dann nur sichergestellt werden, dass die Signale $x(t)$ und $z(t)$ zu den Detektionszeitpunkten übereinstimmen. Man spricht in diesem Zusammenhang von Nyquistsystemen.
Aufgaben zum Kapitel
Aufgabe 2.5: Verzerrung und Entzerrung
Aufgabe 2.5Z: Nyquistentzerrung
Aufgabe 2.6Z: Synchrondemodulator
Aufgabe 2.7: Nochmals Zweiwegekanal