Gesetzmäßigkeiten der Fouriertransformation
Inhaltsverzeichnis
Multiplikation mit Faktor - Additionssatz
In diesem Abschnitt sind die Gesetzmäßigkeiten der Fouriertransformation zusammengestellt. Diese können beispielsweise dazu genutzt werden, um mit möglichst geringem Rechenaufwand aus bereits bekannten Transformationen
$$x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ),\quad x_1 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_1 ( f ),\quad x_2 ( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_2 ( f )$$
neue Funktionszusammenhänge abzuleiten. Wir beschränken uns hier auf reelle Zeitfunktionen.
Ein konstanter Faktor k wirkt sich auf die Zeit– und die Spektralfunktion in gleicher Weise aus:
$$k \cdot x(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,k \cdot X(f).$$
Diesen Zusammenhang kann man zum Beispiel zur Vereinfachung nutzen, indem man die Konstante k (die sowohl ein Verstärkungs– oder ein Einheitenfaktor sein kann) zunächst weglässt und erst später dem Ergebnis wieder hinzufügt.
Obiger Satz folgt unmittelbar aus der Definition des ersten Fourierintegrals, ebenso wie der Additionssatz, der die Grundlage für das so genannte Superpositionsprinzip darstellt.
Kann man eine Zeitfunktion als Summe von Einzelfunktionen schreiben, so ist die resultierende Spektralfunktion die Summe der resultierenden Einzelspektren (Additionssatz):
$$x( t ) = x_1 ( t ) + x_2 ( t )\quad\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\quad X( f ) = X_1 (f) + X_2 ( f ).$$
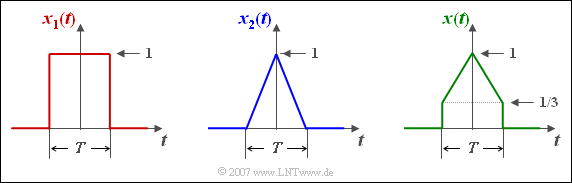
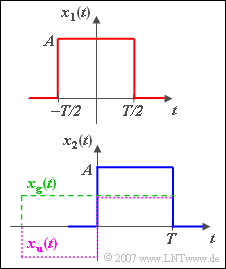
Bekannt sind die beiden Fourierkorrespondenzen
$$ \begin{align*} x_1 ( t )\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\quad X_1 ( f )\hspace{-0.15cm} & = \hspace{-0.15cm} T \cdot {\rm si}(\pi f T),\\ x_2 ( t )\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\quad X_2 ( f )\hspace{-0.15cm} & = \hspace{-0.15cm} T /2\cdot {\rm si}(\pi f T/2).\end{align*}$$
Dann gilt für das Summensignal:
$$x(t) = {1}/{3} \cdot x_1 ( t ) + {2}/{3} \cdot x_2 ( t )\quad \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\quad X ( f ) = {1}/{3} \cdot X_1 ( f ) + {2}/{3} \cdot X_2 ( f ).$$
Zuordnungssatz
Bereits bei der komplexen Fourierreihe zur Beschreibung periodischer Signale haben wir festgestellt, dass eine gerade Funktion stets zu reellen und eine ungerade Funktion ausschließlich zu imaginären Fourierkoeffizienten führt. Die Fouriertransformation zeigt ähnliche Eigenschaften.
Besteht eine reelle Zeitfunktion additiv aus einem geraden und einem ungeraden Anteil,
$$x( t ) = x_{\rm g} ( t ) + x_{\rm u} ( t ),$$
so gilt für die dazugehörige Spektralfunktion (Zuordnungssatz):
$$X(f) = X_{\rm R}(f) + {\rm j}\cdot X_{\rm I}(f),$$ mit $x_{\rm g} (t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X_{\rm R} (f)$ und $x_{\rm u} (t) \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, {\rm j} \cdot X_{\rm I} (f)$.
Der Realteil$X_R(f)$ des Spektrums ist dann ebenfalls gerade, während $X_I(f)$ eine ungerade Funktion der Frequenz beschreibt.
Dieser Satz lässt sich einfach beweisen, wenn man den Satz von Leonhard Euler berücksichtigt:
$${\rm e}^{ - {\rm j}\omega _0 t} = \cos ( {\omega _0 t} ) - {\rm j}\cdot \sin ( {\omega _0 t} ).$$
Den geraden und ungeraden Anteil einer Funktion $x(t)$ kann man mit folgenden Gleichungen berechnen:
$$x_{\rm g} (t) = \frac{1}{2}\left( {x(t) + x(-t)} \right),$$
$$x_{\rm u} (t) = \frac{1}{2}\left( {x(t) - x(-t)} \right).$$
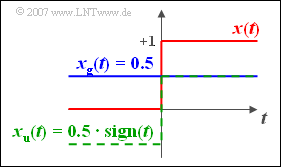
Wir betrachten die Sprungfunktion $y(t)$:
Diese kann wie folgt aufgeteilt werden:
$$x(t) = \gamma (t) = \left\{ \begin{array}{l} 0\quad \quad {\rm f\ddot{u} r}\;t < 0 \\ 1\quad \quad{\rm f\ddot{u} r}\; t > 0 \\ \end{array} \right \}.$$
wobei die Signum-Funktion verwendet wurde:
$${\rm sign} (t) = \bigg\{ \begin{array}{l} -1\quad \quad {\rm f\ddot{u} r}\;t < 0, \\ +1\quad \quad{\rm f\ddot{u} r}\; t > 0. \\ \end{array}$$
Der gerade (blaue) Signalanteil ist eine Konstante mit der reellen Spektralfunktion $0.5 \cdot \delta(f)$. Das Spektrum der ungeraden (grünen) Signumfunktion wurde bereits im Beispiel auf der Seite Fouriertransformation berechnet. Damit erhält man für das resultierende Spektrum von $x(t)$:
$$X(f) = \frac{1}{2} \cdot \delta (f) - {\rm j}\cdot \frac{1}{2\pi f}.$$
Ähnlichkeitssatz
Der Ähnlichkeitssatz zeigt den Zusammenhang zwischen den Spektralfunktionen zweier zwar formgleicher, aber gestreckter oder gestauchter Zeitsignale auf.
Ist $X(f)$ die Fouriertransformierte von $x(t)$, so gilt mit der reellen Konstanten $k$ auch folgender Funktionszusammenhang (Ähnlichkeitssatz):
$$x( {k \cdot t} )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\frac{1}{\left| k \right|} \cdot X( {f}/{k} ).$$
Für positives $k$ folgt aus dem Fourierintegral mit der Substitution $\tau = k \cdot t$:
$$\int_{ - \infty }^{ + \infty } {x( {k \cdot t})} \cdot {\rm e}^{ - {\rm j}2\pi ft} \hspace{0.1cm}{\rm d}t = \frac{1}{k} \cdot \int_{ - \infty }^{ + \infty } {x( \tau )} \cdot {\rm e}^{ - {\rm j}2\pi \cdot f/k \hspace{0.03cm}\cdot \tau } \hspace{0.1cm}{\rm d} \tau = \frac{1}{k}\cdot X( {{f}/{k}}).$$
Für negatives $k$ würden sich die Integrationsgrenzen vertauschen und man erhält $1/(-k) \cdot X(f/k)$. Da in der Gleichung $|k|$ verwendet wird, gilt das Ergebnis für beide Vorzeichen.
Die Auswirkungen des Ähnlichkeitssatzes kann man sich zum Beispiel mit einem Tonband verdeutlichen. Spielt man ein solches Band mit doppelter Geschwindigkeit ab, so entspricht dies einer Stauchung des Zeitsignals ($k$ = 2). Dadurch erscheinen die Frequenzen doppelt so hoch.
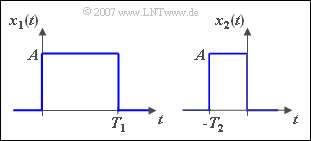Wir betrachten zwei Rechtecke gleicher Höhe, wobei $T_2 = T_1/2$ gilt.
Die Spektralfunktion von $x_1(t)$ ergibt sich nach dem ersten Fourierintegral zu
$$X_1 (f) = A \cdot \frac{{1 - {\rm e}^{ - {\rm j}2\pi fT_1 } }}{{{\rm j}2\pi f}} .$$
Dafür kann auch geschrieben werden:
$$X_1 (f) = A \cdot T_1 \cdot \frac{{{\rm e}^{{\rm j}\pi fT_1 } - {\rm e}^{ - {\rm j}\pi fT_1 } }}{{{\rm j}2\pi fT_1 }} \cdot {\rm e}^{ - {\rm j}\pi fT_1 } = A \cdot T_1 \cdot {\rm si}( {\pi f T_1 } ) \cdot {\rm e}^{ - {\rm j}\pi fT_1 }.$$
Für die Spektralfunktion von $x_2(t)$ folgt aus dem Ähnlichkeitssatz mit $k$ = –2:
$$X_2 (f) = \frac{1}{2} \cdot X_1 ( { - \frac{f}{2}} ) = \frac{A \cdot T_1 }{2} \cdot {\rm si}( { - \pi f\frac{T_1 }{2}} ) \cdot {\rm e}^{{\rm j}\pi fT_1 /2} .$$
Die si-Funktion ist gerade: si(–$x$) = si($x$). Deshalb kann man auf das Vorzeichen im Argument der si-Funktion verzichten. Mit $T_2 = T_1/2$ erhält man schließlich:
$$X_2 (f) = A \cdot T_2 \cdot {\rm si}( {\pi fT_2 } ) \cdot {\rm e}^{ {\rm j}\pi fT_2 } .$$
Reziprozitätsgesetz von Zeitdauer und Bandbreite
Dieses Gesetz folgt direkt aus dem Ähnlichkeitssatz: Je breiter ein Impuls in seiner zeitlichen Ausdehnung ist, desto schmäler und höher ist das zugehörige Spektrum und umgekehrt. Um quantitative Aussagen treffen zu können, definieren wir zwei Kenngrößen für energiebegrenzte Signale ⇒ Impulse:
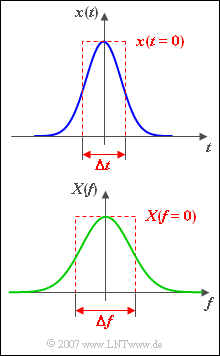
- Die äquivalente Impulsdauer wird aus dem Zeitverlauf abgeleitet. Sie ist gleich der Breite eines flächengleichen Rechtecks mit gleicher Höhe wie $x(t)$:
$$\Delta t = \frac{1}{{x( {t = 0} )}}\int_{ - \infty }^{ + \infty } {x( t)} \hspace{0.1cm}{\rm d}t.$$
- Die äquivalente Bandbreite kennzeichnet den Impuls im $f$–Bereich. Sie gibt die Breite des flächengleichen Rechtecks mit gleicher Höhe wie das Spektrum $X(f)$ an:
$$\Delta f = \frac{1}{{X( {f = 0} )}}\int_{ - \infty }^{ + \infty } {X( f )} \hspace{0.1cm} {\rm d}f.$$
Beide Größen sind nebenstehend für einen Gaußimpuls und dessen ebenfalls gaußförmiges Spektrum dargestellt.
Das Produkt aus äquivalenter Impulsdauer und äquivalenter Bandbreite ist stets gleich 1:
$$\Delta t \cdot \Delta f = 1$$
Man bezeichnet diesen Zusammenhang als Reziprozitätsgesetz.
Ausgehend von den beiden Fourierintegralen erhält man für $f$ = 0 bzw. $t$ = 0:
$$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$
Berücksichtigt man dieses Ergebnis bei obigen Definitionen, so erhält man:
$$X( {f = 0} ) = \int_{ - \infty }^{ + \infty } {x(t)\hspace{0.1cm}{\rm d}t,} \hspace{0.5cm}x( {t = 0} ) = \int_{ - \infty }^{ + \infty } {X(f)\hspace{0.1cm}{\rm d}f.}$$
Daraus folgt direkt $\Delta t \cdot \Delta f = 1$.
Anzumerken ist, dass $\Delta f$ über das tatsächliche Spektrum $X(f)$ und nicht über $|X(f)|$ definiert ist. Bei reellen Funktionen genügt die Integration über den geraden Funktionsanteil, da das Integral über den ungeraden Anteil wegen des Zuordnungssatzes stets 0 ist. Bei ungeraden Zeitfunktionen und damit rein imaginären Spektren versagen die beiden Definitionen von $\Delta t$ bzw. $\Delta f$.
Verbreitert man den Gaußimpuls um den Faktor 3, so wird die äquivalente Bandbreite um den gleichen Faktor kleiner. Da die Impulsamplitude $x(t = 0)$ nicht verändert wird, bleibt auch die Integralfläche über $X(f)$ konstant. Das heißt, dass $X(f=0)$ gleichzeitig um den Faktor 3 größer wird.
Vertauschungssatz
Diese Gesetzmäßigkeit ist besonders nützlich, um neue Fourierkorrespondenzen zu erhalten.
Ist $X(f)$ die Fouriertransformierte von $x(t)$, dann gilt nach dem Vertauschungssatz auch:
$$X^{\star}(t)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,x^{\star}( f ).$$
Beschränken wir uns auf reelle Zeitfunktionen, so können die Zeichen für „konjugiert komplex” auf beiden Seiten der Fourierkorrespondenz weggelassen werden.
Das erste Fourierintegral lautet nach sukzessiver Umbenennung $t \to u$ bzw. $f \to t$:
$$X( f ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}2\pi fu} \hspace{0.1cm}{\rm d}u, \hspace{1cm} X(t ) = \int_{ - \infty }^{ + \infty } {x( u )} \cdot {\rm e}^{ - {\rm j}2\pi tu}\hspace{0.1cm} {\rm d}u.$$
Ändert man das Vorzeichen in den Exponenten, so muss man $X(t)$ durch $X^*(t)$ und $x(u)$ durch $x^*(u)$ ersetzen:
$$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( u )} \cdot {\rm e}^{ {\rm j}2\pi tu}\hspace{0.1cm} {\rm d}u.$$
Mit der weiteren Umbennung $u \to f$ kommt man zum zweiten Fourierintegral:
$$X^{\star}(t ) = \int_{ - \infty }^{ + \infty } {x^{\star}( f )} \cdot {\rm e}^{ {\rm j}2\pi ft}\hspace{0.1cm} {\rm d}f.\hspace{7.9cm}$$
Das Spektrum $X(f) = \delta(f)$ des Gleichsignals $x(t)$ = 1 wird als bekannt vorausgesetzt. Nach dem Vertauschungssatz lautet deshalb die Spektralfunktion des Diracimpulses $x(t) = \delta(t)$:
$$ x(t) = \delta(t)\hspace{0.1cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.1cm} X(f)= 1.$$
Die folgende Grafik zeigt eine weitere Anwendung des Vertauschungssatzes.
Verschiebungssatz
Betrachten wir nun eine Verschiebung der Zeitfunktion – z. B. verursacht durch eine Laufzeit – oder eine Frequenzverschiebung, wie sie beispielsweise bei der Amplitudenmodulation auftritt.
Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) der Zeitfunktion $x(t)$, so gelten nach dem Verschiebungssatz auch folgende Zusammenhänge:
$$x( {t - t_0 } )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f ) \cdot {\rm e}^{ - {\rm j}2\pi ft_0 },$$
$$x( t ) \cdot {\rm e}^{ {\rm j}2\pi f_0 t}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( {f - f_0 } ).$$
Hierbei sind $t_0$ und $f_0$ Zeit– bzw. Frequenzgrößen.
Beweis von Gleichung (1): Das erste Fourierintegral für das um $t_0$ nach rechts verschobene Signal $x_V(t) = x(t-t_0)$ lautet mit der Substitution $\tau = t - t_0$:
$$X_{\rm V} ( f ) = \int_{ - \infty }^{ + \infty } {x( {t - t_0 } ) \cdot {\rm e}^{ - {\rm j}2\pi ft}\hspace{0.1cm}{\rm d}t} = \int_{ - \infty }^{ + \infty } {x( \tau ) \cdot {\rm e}^{ -{\rm j}2\pi f( {\tau + t_0 } )}\hspace{0.1cm} {\rm d}\tau .}$$
Der von der Integrationsvariablen $\tau$ unabhängige Term kann vor das Integral gezogen werden. Mit der Umbennung $\tau /to t$ erhält man dann:
$$X_{\rm V}( f ) = {\rm e}^{ - {\rm j}2\pi ft_0 } \cdot \int_{ - \infty }^{ + \infty } {x( t )} \cdot {\rm e}^{ - {\rm j}2\pi ft}\hspace{0.1cm} {\rm d}t = {\rm e}^{ - {\rm j}2 \pi ft_0 } \cdot X( f).$$
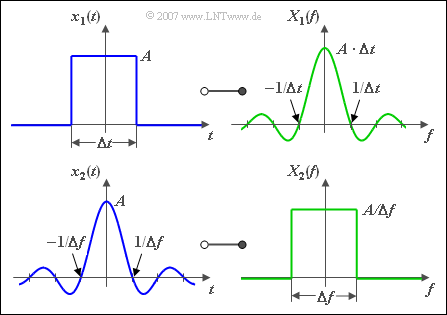
Wie bereits erwähnt, besitzt der symmetrische Rechteckimpuls $x_1(t)$ das folgende Spektrum:
$$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ).$$
Der unten dargestellte Rechteckimpuls $x_2(t)$ ist gegenüber $x_1(t)$ um $T/2$ nach rechts verschoben: $x_2(t) = x_1(t-T/2)$. Somit lautet sein Spektrum:
$$X_2( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\pi fT} .$$
Diese Spektralfunktion kann mit dem Eulerschen Satz und einiger einfacher trigonometrischer Umformungen auch wie folgt geschrieben werden:
$$X_2( f ) = \frac{A }{2\pi f} \cdot \sin ( 2\pi fT) + {\rm j}\cdot \frac{A }{2\pi f} \cdot \left[ {\cos ( {2\pi fT} ) - 1} \right] .$$
Das gleiche Ergebnis erhält man auch mit dem Zuordnungssatz: Der Realteil des Spektrums gehört zum geraden Signalanteil $x_g(t)$, der Imaginärteil zum ungeraden Anteil $x_u(t)$.
Differentiationssatz
Dieser Satz zeigt, wie sich die Differentiation einer Funktion (im Zeit– bzw. Frequenzbereich) in der korrespondierenden Fouriertransformierten auswirkt; er ist auch mehrfach anwendbar. Ein einfaches Beispiel für die Anwendung dieses Satzes ist der Zusammenhang zwischen dem Strom $i(t)$ und der Spannung $u(t)$ einer Kapazität $C$: $i(t) = C \cdot \text{d}u(t)/\text{d}t$.
Ist $X(f)$ die Fouriertransformierte von $x(t)$, so gelten auch folgende Korrespondenzen:
$$\frac{{{\rm d}x( t )}}{{{\rm d}t}}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,{\rm j}2\pi f \cdot X( f ),$$
$$- t \cdot x( t )\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\frac{1}{{{\rm j}2\pi }} \cdot \frac{{{\rm d}X( f )}}{{{\rm d}f}}.$$
Dies sind die beiden Varianten des Differentiationsssatzes.
Die erste Gleichung ergibt sich durch Differentiation des zweiten Fourierintegrals:
$$y(t) = \frac{\text{d}x(t)}{\text{d}t} = \frac{\text{d}}{\text{d}t}\int_{ - \infty }^{ + \infty } X( f ) \cdot {\rm e}^{{\rm j}2\pi ft}\hspace{0.1cm} {\rm d}f = \int_{ - \infty }^{ + \infty } {X( f )} \cdot {\rm j}2\pi f \cdot {\rm e}^{{\rm j}2\pi ft} {\rm d}f.$$
Gleichzeitig gilt aber auch:
$$y( t ) = \int_{ - \infty }^{ + \infty } {Y( f )} \cdot {\rm e}^{{\rm j}2\pi ft}\hspace{0.1cm} {\rm d}f.$$
Durch Vergleich der Integranden erhält man die obere Variante des Differentiationssatzes. Zur Herleitung der zweiten Variante geht man ausgehend vom ersten Fourierintegral in analoger Weise vor. Der negative Exponent im ersten Fourierintegral führt zum Minuszeichen in der Zeitfunktion.
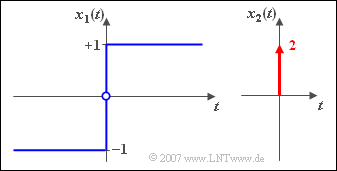Die Spektren der skizzierten Signale $x_1(t)$ und $x_2(t)$ wurden bereits in früheren Beispielen wie folgt berechnet:
$$\begin{align*} X_1( f ) & = \frac{1 }{{\rm j\pi} f}, \\ X_2( f ) & = 2 = {\rm const.}\end{align*} $$
Offensichtlich gilt $X_2(f) = X_1(f) \cdot j2\pi f$.
- Aus dem Differentiationssatz folgt somit, dass $x_2(t)$ gleich der Ableitung von $x_1(t)$ nach der Zeit ist. Dies stimmt tatsächlich: Für $t \neq 0$ ist $x_1(t)$ konstant, also die Ableitung 0.
- Bei $t=0$ ist die Steigung unendlich groß, was sich auch in der Gleichung $x_2(t) = 2 \cdot \delta(t)$ ausdrückt. Das Impulsgewicht „2” der Diracfunktion berücksichtigt, dass der Sprung innerhalb der Funktion $x_1(t)$ bei $t$ = 0 die Höhe 2 hat.
Integrationssatz
Die Integration ist ebenso wie die Differentiation eine lineare Operation. Daraus ergibt sich:
Ist $X(f)$ die Fouriertransformierte (Spektralfunktion) von $x(t)$, so gelten auch die folgenden Fourierkorrespondenzen (Integrationssatz):
$$\int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right),$$
$$x( t )\left( { - \frac{1}{{{\rm j}2\pi t}} + \frac{1}{2}\cdot \delta ( t )} \right)\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\int_{ - \infty }^f {X( \nu ) \hspace{0.1cm}{\rm d}\nu .}$$
Da der Integrationssatz genau die Umkehrung des Differentiationssatzes darstellt, soll hier auf den Beweis verzichtet und stattdessen auf [Mar94] verwiesen werden. Wendet man auf die obere Gleichung den Differentiationssatz an, so erhält man:
$$\frac{ {\rm d}}{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}2\pi f.$$
Die Differentiation nach der oberen Grenze auf der linken Seite liefert genau den Integranden $x(t)$. Auf der rechten Seite der Korrespondenz ergibt sich richtigerweise $X(f)$, da die Diracfunktion bei $f=0$ wegen der Multiplikation mit $\text{j}2\pi f$ ausgeblendet wird. Alle im Kapitel 3.3 dargelegten Gesetzmäßigkeiten – unter Anderem auch der Differentiations– und der Integrationssatz – werden in einem Lernvideo an Beispielen verdeutlicht: Gesetzmäßigkeiten der Fouriertransformation (Dauer Teil 1: 5:57 – Teil 2: 5:55)
$$\frac{ {\rm d}}{ {\rm d}t} \int_{ - \infty }^{\hspace{0.05cm}t} {x( \tau )} \hspace{0.1cm}{\rm d}\tau\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,X( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right) \cdot {\rm j}2\pi f.$$
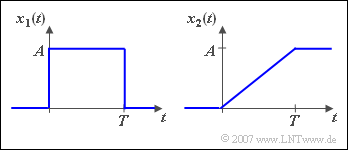
Die skizzierten Signale $x_1(t)$ und $x_2(t)$ hängen wie folgt zusammen:
$$x_2( t ) = \frac{1}{T}\int_{ - \infty }^{\hspace{0.05cm}t} {x_1 } ( \tau )\hspace{0.1cm}{\rm d}\tau .$$
Aufgrund des Integrationssatzes gilt der Zusammenhang zwischen den Spektren:
$$X_2 ( f ) = \frac{1}{T}\cdot X_1 ( f )\left( {\frac{1}{{{\rm j}2\pi f}} + \frac{1}{2}\cdot \delta ( f )} \right).$$
Mit der Spektralfunktion
$$X_1 ( f ) = A \cdot T \cdot {\rm si}( {\pi fT} ) \cdot {\rm e}^{ - {\rm j}\pi fT}$$
erhält man somit
$$X_2 ( f ) = \frac{ {A }}{2}\cdot \delta ( f ) + \frac{ {A \cdot T}}{{2{\rm j}}} \cdot \frac{ {\sin( {\pi fT})}}{{\left( {\pi fT} \right)^2 }} \cdot {\rm e}^{ - {\rm j}\pi fT},$$
bzw. nach trigonometrischen Umformungen:
$$X_2 ( f ) = \frac{ {A}}{2}\cdot \delta ( f ) + \frac{ {A \cdot T}}{{( {2\pi fT} )^2 }}\cdot \left[ {\cos( {2\pi fT} ) - 1 - {\rm j}\cdot \sin ( {2\pi ft} )} \right].$$
Hierzu ist anzumerken:
- Die Diracfunktion bei $f$ = 0 mit dem Gewicht $A/2$ berücksichtigt den Gleichanteil der Rampenfunktion $x_2(t)$. Das bedeutet auch: Der Gleichanteil der Rampenfunktion ist genau so groß wie der Gleichanteil der Sprungfunktion.
- Das fehlende Dreieck mit den Eckpunkt–Koordinaten (0, 0), ($T$, $A$) und (0, $A$) ändert am Gleichanteil nichts; es wirkt sich gegenüber der unendlich großen Restfläche nicht aus.
Aufgaben zum Kapitel
A3.4 Trapezspektrum bzw. -impuls
Z3.4 Trapez, Rechteck und Dreieck
A3.5 Differentiation eines Dreicksignals
Z3.5 Integration von Diracfunktionen
A3.6 Gerades/ungerades Zeitsignal
